Пусть случайная величина X имеет нормальное распределение с неизвестным математическим ожиданием 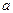 и известной дисперсией s2. Пусть произведено n независимых опытов и на основании статистических данных получено выборочное среднее:
и известной дисперсией s2. Пусть произведено n независимых опытов и на основании статистических данных получено выборочное среднее: 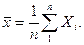
Задаем достаточно высокую доверительную вероятность g. Требуется построить доверительный интервал 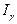 . Прежде всего, заметим, что случайная величина
. Прежде всего, заметим, что случайная величина 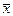 также имеет нормальное распределение
также имеет нормальное распределение 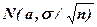 . Действительно,
. Действительно,
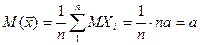 ;
; 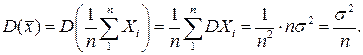
Вероятность попадания случайной величины 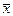 с нормальным законом распределения в симметричный интервал с центром в точке
с нормальным законом распределения в симметричный интервал с центром в точке 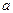 и радиусом ε равен
и радиусом ε равен
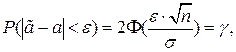
где 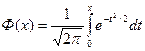 – функция Лапласа.
– функция Лапласа.
Обозначая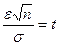 , имеем Ф (t) = g/2. Затем по табл. 4 приложения находим t по значению Ф (t) = g/2; отсюда находится
, имеем Ф (t) = g/2. Затем по табл. 4 приложения находим t по значению Ф (t) = g/2; отсюда находится 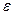 :
: 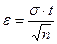 . Таким образом, доверительный интервал имеет вид
. Таким образом, доверительный интервал имеет вид

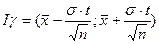 .
.
Задача. Случайная величина X имеет нормальное распределение с известным s=3. Найти доверительный интервал для оценки неизвестного математического ожидания а по его выборочному среднему 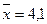 , если известны объем выборки
, если известны объем выборки 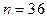 и
и 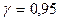 .
.
Решение. Имеем
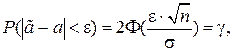 t =
t = 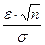 ,
, 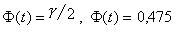 .
.
Из табл. 4 t = 1,96. Тогда 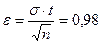 . Таким образом,
. Таким образом,
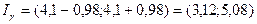 .
.
2. Доверительный интервал для оценки математического ожидания
нормального распределения с неизвестным s
В отличие от предыдущего, случайная величина X имеет нормальное распределение N (a,s) с неизвестным s. Пусть произведено n независимых испытаний, построены выборочная средняя 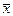 и “исправленная” выборочная дисперсия S 2. Требуется построить доверительный интервал для оценки
и “исправленная” выборочная дисперсия S 2. Требуется построить доверительный интервал для оценки 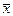 математического ожидания.
математического ожидания.
Рассмотрим случайную величину
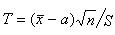 .
.
Распределение является t – распределение или распределением Стьюдента с 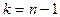 степенями свободы.
степенями свободы.
Действительно, по определению, если 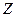 – случайная величина с нормальным распределением
– случайная величина с нормальным распределением 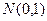 , а V – случайная величина, распределенная по закону c2 с k степенями свободы, то случайная величина
, а V – случайная величина, распределенная по закону c2 с k степенями свободы, то случайная величина 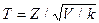 распределена по закону Стьюдента с k степенями свободы.
распределена по закону Стьюдента с k степенями свободы.
Случайная величина 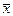 распределена по нормальному закону
распределена по нормальному закону 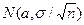 . Случайная величина
. Случайная величина
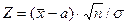
распределена также по нормальному закону (как линейная функция относительно нормального аргумента 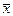 ) с законом
) с законом 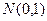 .
.
Известно, что случайная величина
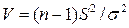
распределена по закону c2 с 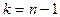 степенями свободы. Поэтому случайная величина T распределена по закону Стьюдента.
степенями свободы. Поэтому случайная величина T распределена по закону Стьюдента.
С ростом степеней свободы распределение Стьюдента приближается к нормальному 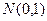 и уже при
и уже при 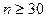 практически не отличается от него. Следовательно, при оценке неизвестных параметров по выборке малого объема
практически не отличается от него. Следовательно, при оценке неизвестных параметров по выборке малого объема 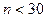 используют распределение Стьюдента При построении доверительного интервала для математического ожидания речь идет о вероятности Имеем
используют распределение Стьюдента При построении доверительного интервала для математического ожидания речь идет о вероятности Имеем
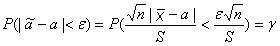 или с учетом
или с учетом
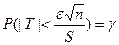 .
.
Обозначая 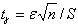 , получаем
, получаем 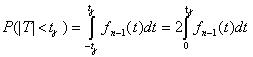 .
.
Таким образом, имеем
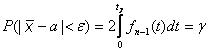 .
.
Значение 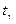 определяется по вероятности
определяется по вероятности 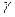 из табл. 5 приложения распределения Стьюдента. Затем, принимая во внимание, что
из табл. 5 приложения распределения Стьюдента. Затем, принимая во внимание, что 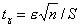 , находим
, находим 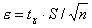 . Таким образом, доверительный интервал для оценки математического ожидания с неизвестным s имеет вид
. Таким образом, доверительный интервал для оценки математического ожидания с неизвестным s имеет вид
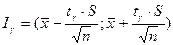 .
.
Задача 5.3.2. Случайная величина X имеет нормальное распределение. По выборке объемом n = 15 найдены выборочная средняя 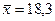 , “исправленное” среднее квадратическое отклонение
, “исправленное” среднее квадратическое отклонение 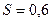 . Определить интервальную оценку математического ожидания с доверительной вероятностью
. Определить интервальную оценку математического ожидания с доверительной вероятностью 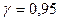 .
.
Решение. По табл. 5 приложения находим 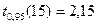 . Тогда
. Тогда 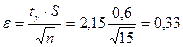 . По формуле (5.3.11) получим доверительный интервал
. По формуле (5.3.11) получим доверительный интервал
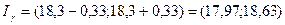 .
.
Замечание. Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение которой 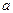 неизвестно и которая имеет нормальное распределение. Пусть
неизвестно и которая имеет нормальное распределение. Пусть 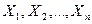 – результаты отдельных измерений, рассматриваемые как независимые случайные величины с одним и тем распределением, и имеют одно и то же математическое ожидание (истинное значение измеряемой величины), одинаковые дисперсии s2 (измерения равноточные). В этом случае истинное значение измерений физической величины оценивается с помощью среднего выборочного
– результаты отдельных измерений, рассматриваемые как независимые случайные величины с одним и тем распределением, и имеют одно и то же математическое ожидание (истинное значение измеряемой величины), одинаковые дисперсии s2 (измерения равноточные). В этом случае истинное значение измерений физической величины оценивается с помощью среднего выборочного 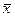 , для которого можно построить доверительный интервал (с неизвестным s) по методу, указанному в п. 2.
, для которого можно построить доверительный интервал (с неизвестным s) по методу, указанному в п. 2.
Задача 5.3.3. По данным 16-ти независимых равноточных измерений физической величины найдено выборочное среднее 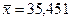 и “исправленное” среднее квадратическое отклонение
и “исправленное” среднее квадратическое отклонение 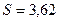 . Требуется оценить истинное значение случайной величины с надежностью
. Требуется оценить истинное значение случайной величины с надежностью 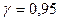 .
.
Решение. Истинное значение измеряемой величины равно ее математическому ожиданию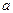 . Поэтому задача сводится к оценке математического ожидания (при неизвестном s) для нормального распределения с помощью доверительного интервала. Доверительный интервал находится с помощью формулы (5.3.11).
. Поэтому задача сводится к оценке математического ожидания (при неизвестном s) для нормального распределения с помощью доверительного интервала. Доверительный интервал находится с помощью формулы (5.3.11).
Используя табл. 5 приложения по 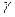 =0,95 и
=0,95 и 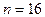 , находим
, находим 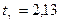 . Имеем
. Имеем
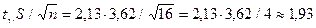 ,
,
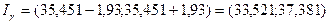 .
.
 2014-02-12
2014-02-12 12371
12371
