Пусть исследуется случайная величина X с математическим ожиданием 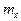 . Обозначим через x 1, x 2,..., x n значения случайной величины, полученные в результате n независимых равноточных опытов, т.е. измерений, которые проводились в одинаковых условиях. В качестве оценки для
. Обозначим через x 1, x 2,..., x n значения случайной величины, полученные в результате n независимых равноточных опытов, т.е. измерений, которые проводились в одинаковых условиях. В качестве оценки для 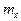 примем среднее арифметическое наблюдаемых значений
примем среднее арифметическое наблюдаемых значений
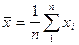 .
.
 в дальнейшем принято называть выборочной средней.
в дальнейшем принято называть выборочной средней.
Оценка является несмещенной, так как  .
.
Оценка является состоятельной, так как по теореме Чебышева (частный случай) имеем  при
при 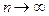 .
.
Эффективность оценки (5.2.7) выполняется лишь для узкого класса распределений, в частности, для нормального распределения 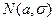 .
.
 2014-02-12
2014-02-12 603
603








