Прямые частного положения в плоскости

В каждой плоскости можно провести бесчисленное множество прямых линий частного положения.

Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций p₁. Она обладает всеми свойствами горизонтальной прямой: ее фронтальная проекция параллельна оси x, а на горизонтальную плоскость проекций она проецируется в истинную величину (рис. 39).

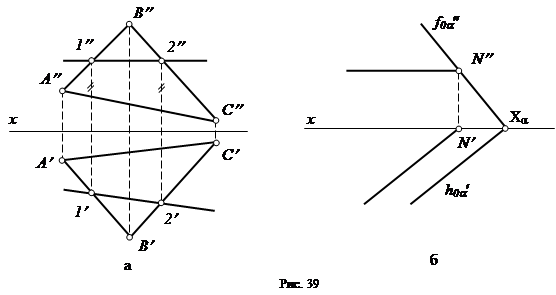Если плоскость задана следами (рис. 39, б), то горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали параллельна оси x, а фронтальная проекция – есть ее истинная величина (рис. 40).

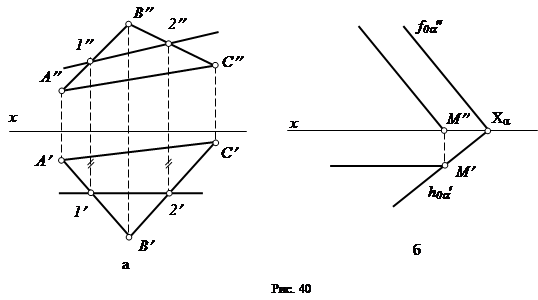Фронтальная проекция фронтали параллельна фронтальному следу плоскости, в которой лежит данная фронталь. (рис. 40, б).

ЛИНИЯ НАИБОЛЬШЕГО СКАТА ПЛОСКОСТИ

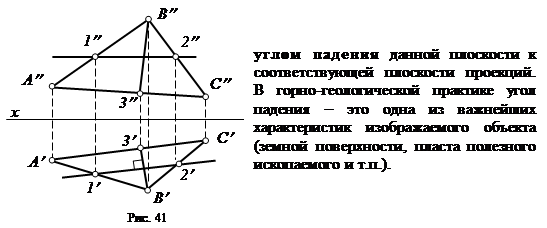
Линия наибольшего ската – это прямая, лежащая в плоскости и перпендикулярная следу или линиям частного положения плоскости (в нашем примере на рис. 41 – перпендикулярная горизонталям этой плоскости).

Из всех прямых, принадлежащих плоскости, линия наибольшего ската имеет самый большой угол наклона к соответствующей плоскости проекций (в нашем примере на рис. 41 – к горизонтальной плоскости проекций p₁), который называется

ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

Рассмотрим пример: через точку К провести прямую, параллельную плоскости a, заданной следами (рис. 42).

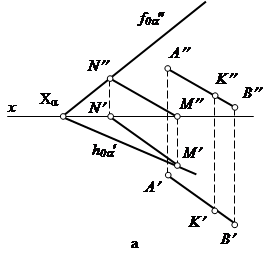
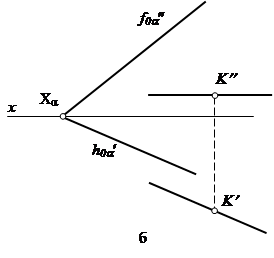Проведем в плоскости a любую прямую, например, прямую MN (рис. 42, а). Затем через точку К параллельно MN проведем прямую АВ. Эта прямая будет параллельна плоскости a, так как она параллельна прямой MN, лежащей в этой плоскости.

	Рис. 42

Эту же задачу, можно решить другим способом, проведя через точку К прямую частного положения, например, горизонтальную прямую (рис. 42, б). Горизонтальная проекция горизонтальной прямой проходит через проекцию К ¢ и параллельна следу h _0a¢.

Если плоскость задана не следами, а иным способом (двумя пересекающимися прямыми, двумя параллельными прямыми, плоской фигурой и т.д.), то через заданную точку также можно провести прямую, параллельную любой прямой, лежащей в заданной плоскости. В качестве такой прямой может быть выбрана одна из прямых,

которыми задана сама плоскость.

ТОЧКА В ПЛОСКОСТИ

Точка лежит в плоскости, если она лежит на прямой, принадлежащей этой плоскости.

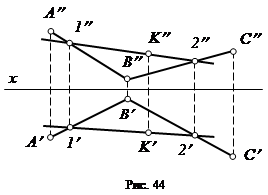Пример 5. Построить недостающую проекцию точки К, лежащей в заданной плоскости (плоскость задана двумя пересекающимися прямыми АВ и ВС, а точка – только ее фронтальной проекцией К ¢¢, рис. 44).

1. Через точку К проведем произвольную прямую 1 - 2, принадлежащую заданной плоскости:

К ¢¢ Î 1 ¢¢ 2 ¢¢.

2. Построим горизонтальные проекции точек 1 ¢ и 2 ¢.

3. Через 1 ¢ и 2 ¢ проводим горизонтальную проекцию прямой 1 - 2.

4. В пересечении линии проекционной связи, проведенной из К ¢¢ и 1 ¢- 2 ¢ находим горизонтальную проекцию точки К.

Если плоскость задана следами, то недостающая проекция точки, принадлежащей заданной плоскости, может быть найдена при помощи горизонтали (рис. 45, а) или фронтали (рис. 45, б) плоскости.