Для всех функциональных зон используется декартова система координат.
Рассматривается плоский длинный прямоугольный канал, полученный развертыванием винтового канала на плоскость.
Используется принцип обращенного движения, когда мысленно останавливается шнек, а цилиндрический корпус вращается с той же угловой скоростью.
Таким образом, процессы тепло- массопереноса моделируются в длинном прямоугольном канале шириной W и высотой H, когда верхняя стенка канала движется с постоянной скоростью (окружной) под углом q к оси канала z.
Принцип обращенного движения.
I. 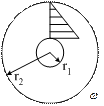
| Движется в направлении оси q.
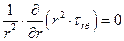
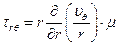
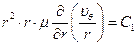
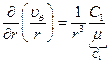 (7.1) (7.1)
|
II. 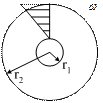
|
Получим выражение для скорости в общем случае, проинтегрируем уравнение (7.1)
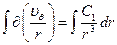
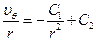 (число 3 – в постоянной C1)
(число 3 – в постоянной C1)
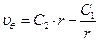
Подставив граничные условия для I и II-го случаев, найдём распределение скоростей:
| I вариант. | II вариант. |
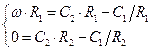
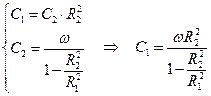
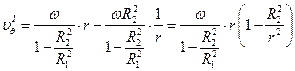
| 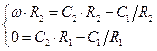
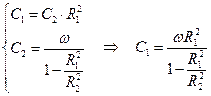
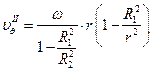
|
Введем соотношения:
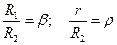 , тогда
, тогда
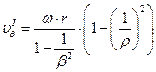 ;
; 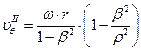
Еще преобразуем:
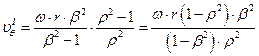
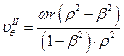
Гипотеза обращенного движения справедлива для случая, когда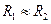 . (то есть глубина канала мала по сравнению с радиусом), то есть
. (то есть глубина канала мала по сравнению с радиусом), то есть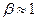 . Очевидно, что правомерность гипотезы будет доказана, если эпюры скоростей при наложении друг на друга дадут ноль (поскольку скорости имеют разные знаки).
. Очевидно, что правомерность гипотезы будет доказана, если эпюры скоростей при наложении друг на друга дадут ноль (поскольку скорости имеют разные знаки).
Сравним числители полученных выражений для скоростей (знаменатели одинаковы).
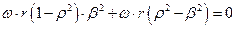
Должны получить тождество:
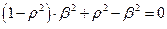 , при
, при 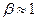 , получим:
, получим:
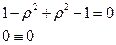
Тождество доказано.
Принцип обращённого движения существенно упрощает задачу. В частности, в задачах течения и теплообмена в канале экструдера это позволяет рассматривать канал, три стенки которого неподвижны, а верхняя граница (поверхность корпуса экструдера) движется.
 2014-02-12
2014-02-12 595
595








