Задача об охлаждении изолированного провода.
Более сложной, чем задача об охлаждении изолированного провода, является задача об охлаждении цилиндра с изоляцией. Подобные задачи с тесным контактом разнородных материалов называют контактными задачами.
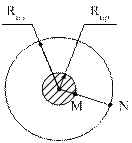
| Рассмотрим проводник с изоляцией: радиус проводника – Rпр; радиус по изоляции - Rиз.
Характеристика проводника: 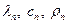 ;
Характеристика изоляции: ;
Характеристика изоляции: 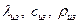 ;
Характеристика внешней среды: ;
Характеристика внешней среды: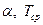 .
Провод движется по охлаждающим ваннам со скоростью u0. .
Провод движется по охлаждающим ваннам со скоростью u0.
|
Задача охлаждения проводника с пластмассовой изоляцией может быть решена в различных вариантах в зависимости от делаемых при постановках задачи допущений.
Допущения:
1. Процесс стационарный.
2. Теплофизические характеристики постоянны.
3. Диффузия тепла в направлении оси Z равна нулю.
4. Температура проводника считается постоянной.
Постановка задачи:
Уравнение энергии:
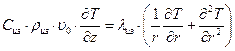
Краевые условия:
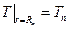
Теплообмен на границе:
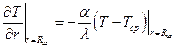
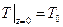
Задача поставлена.
Введём сетку по r и z и запишем производные, входящие в уравнения и Г.У. в разностном виде:
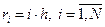 (разбиваем так, чтобы узел попал в точку M)
(разбиваем так, чтобы узел попал в точку M)
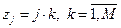
Явная разностная схема:
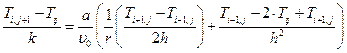 , где (6.1)
, где (6.1)
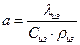 - коэффициент температуропроводности.
- коэффициент температуропроводности.
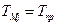 (6.2)
(6.2)
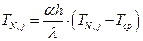 (6.3)
(6.3)
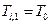 (6.4)
(6.4)
Задача: разностное соотношение (6.1), краевые условия (6.2), (6.3), (6.4).
Решение: из уравнения (6.1) выражаем неизвестное 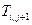 :
:
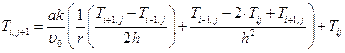 (6.5)
(6.5)
Выражение (63) используется для вычисления температуры во внутренних точках изоляции, для 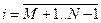
Для расчета температуры на следующем сечении по длине сначала по выражениям (6.2), (6.3), (6.4) перевычисляем значения температуры на границе, далее по выражению (6.5) вычисляем новые значения температур в новом сечении, подставляя в правую часть температурное поле с предыдущего сечения по длине.
В результате получают поле распределения температур по сечению изоляции и по длине изоляции.
Изменения значения технологических параметров, из задачи динамики вязкой жидкости определяют длину ванны, на выходе из которой достигнута нужная температура 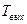 . Варьируя величинами
. Варьируя величинами 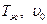 можно получить оптимальную длину ванны с учётом равномерного охлаждения.
можно получить оптимальную длину ванны с учётом равномерного охлаждения.
Модель №2. Отличается от модели 1 тем, что исключается допущение о постоянстве температуры провода.
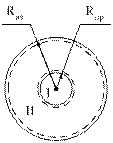
| Имеем две области: I и II.
Для провода:
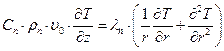 Для изоляции:
Для изоляции:
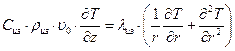
| (6.6) (6.7) |
Краевые условия:
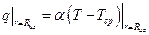 , или
, или 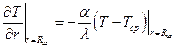 (6.8)
(6.8)
ГУ 4 рода – равенство потоков тепла:
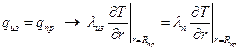 (6.9)
(6.9)
Для области (I):
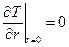 , так как симметричная задача. (6.10)
, так как симметричная задача. (6.10)
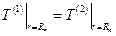 ((1) - со стороны провода; (2) - со стороны изоляции). (6.11)
((1) - со стороны провода; (2) - со стороны изоляции). (6.11)
Задача поставлена.
Решение:
1. Выбираем сетку по радиусу:

| 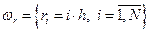 , но 2 области: , но 2 области:
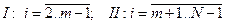
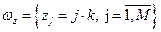 - по длине - по длине
|
2. ГУ по Z:
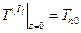 (6.12)
(6.12)
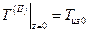 (6.13)
(6.13)
3. Все производные заменяем разностными соотношениями:
Из уравнения (6.6):
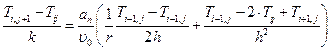 - явная схема,
- явная схема, 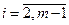 (6.14)
(6.14)
Из уравнения (6.7):
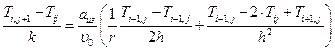 ,
,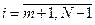 (6.15)
(6.15)
Из уравнения (6.8):
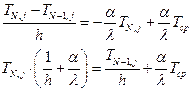
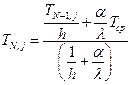 (6.16)
(6.16)
Из уравнения (6.9):
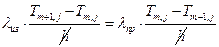
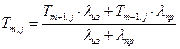 (6.17)
(6.17)
Из уравнения (6.10):
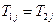 (6.18)
(6.18)
Из уравнения (6.11): Узел ставим на границу ® выполняется автоматически:
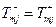 (слева и справа)
(слева и справа)
Расчет:
1. Из уравнений (72) и (73) выделяем неизвестное:
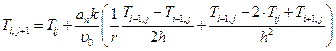
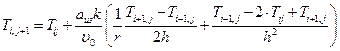
и считаем температуру во внутренних точках области (I) и области (II)
Температуры на границах областей берутся из начальных распределений температур.
2. При расчете температуры на следующем шаге по длине сначала пересчитываются значения температур по уравнениям (6.16¸6.18) в граничных точках через температурное поле, полученное на предыдущих сечениях. Процесс расчета продолжается до конца охлаждающей ванны.
Модель №3. Отличается от второй модели отсутствием допущения о постоянстве теплофизических характеристик.
Пусть как в модели 1 рассматривается уравнение энергии только для изоляции. То есть сохраняется предположение о 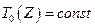 для проводника. Но считается, что
для проводника. Но считается, что 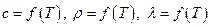 - есть функции температуры, а следовательно, координат.
- есть функции температуры, а следовательно, координат.
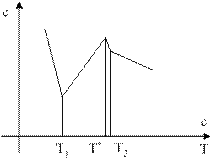
В этом случае кривые изменения 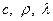 аппроксимируются ломаными линиями на некоторых диапазонах температур. К примеру, график зависимости
аппроксимируются ломаными линиями на некоторых диапазонах температур. К примеру, график зависимости 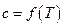 будет выглядеть так:
будет выглядеть так:
| 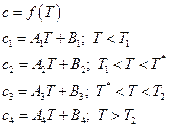 Аналогично аппроксимируются
Аналогично аппроксимируются 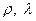
|
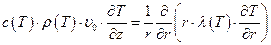 - вторая область (изоляция).
- вторая область (изоляция).
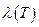 можно вынести из под знака дифференциала в том случае, если для решения используется метод секущих модулей (итерация в каждой точке по координате).
можно вынести из под знака дифференциала в том случае, если для решения используется метод секущих модулей (итерация в каждой точке по координате).
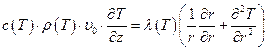
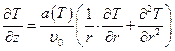
Краевые условия те же, что и в модели 2.
Сетка:
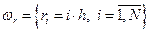 ,
, 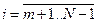
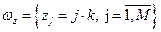
Неявная схема:
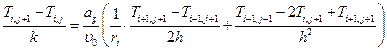
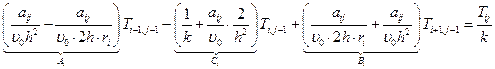 (6.19)
(6.19)
Шаблон:
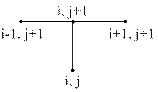
Алгоритм решения:
1. На первом шаге по длине по уравнению (6.19) и уравнению для металла из модели 2 рассчитывается поле температур во внутренних точках областей I и II.
2. Пересчитываются температуры в граничных точках.
3. Пересчитываются значения теплофизических констант по выбранным формулам во всех точках области.
4. Оценивается итерационная погрешность:
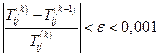 , где k – номер текущей итерации
, где k – номер текущей итерации
При выполнении условия сходимости по итерации, переходят к расчету температурного поля в следующем сечении по длине. Процедура расчета повторяется снова.
Консервативная разностная схема.
Пример:
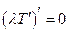
Попробуем решить, используя известные разностные соотношения:
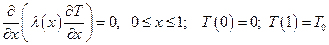
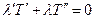
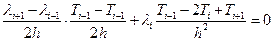
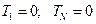
Это уравнение никогда не дает результат, так как начинаются накапливаться ошибки (с точки зрения математики, а с точки зрения физики – появляется новый источник тепла).
Разностные схемы, на которых не выполняются законы сохранения, называются неконсервативными.
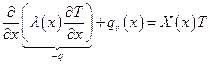 (6.20)
(6.20)
Уравнение (6.20) – уравнение теплопроводности стержня с равномерным внутренним источником тепла.
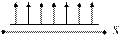
| 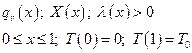
|
Разностные схемы, на которых выполняются законы сохранения, называются консервативными.
При написании консервативной разностной схемы для уравнения (6.20) требуется, чтобы закон сохранения энергии выполнялся для каждой элементарной ячейки сеточной области.
Проинтегрируем уравнение (6.20) на отрезке 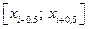
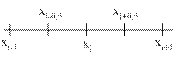
| Будем считать, что в пределах выбранного отрезка температура постоянна: 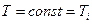
|
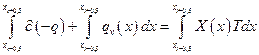
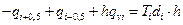 (6.21)
(6.21)
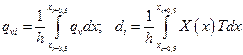
Рассмотрим отрезок 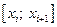
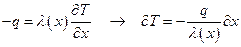 (6.22)
(6.22)
Выражение (6.22) проинтегрируем на отрезке 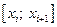 :
:
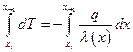
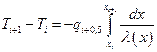
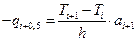 (6.23)
(6.23)
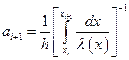
Для того, чтобы получить значение потока в точке 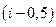 рассмотрим отрезок
рассмотрим отрезок 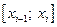 и проинтегрируем выражение (6.22) на этом отрезке:
и проинтегрируем выражение (6.22) на этом отрезке:
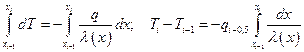
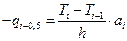 (6.24)
(6.24)
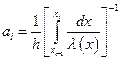
Подставим выражения (6.23) и (6.24) в уравнение (6.21):
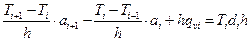
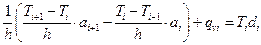 (6.25)
(6.25)
Выражение (6.25) представляет собой консервативную разностную схему исходного уравнения (6.20), в которой в выражениях ai+1 и ai учитывается зависимость теплопроводности от температуры, реализуемая различными способами.
Метод получения выражения (6.25) называется интегро-интерполяционным.
Общая задача течения в кабельной головке с учетом неизотермичности и аномальной вязкости.
Постановка задачи. Задача стационарная, установившаяся, неизотермичная.
Уравнение движения:
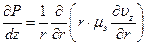 (6.26)
(6.26)
Уравнение энергии:
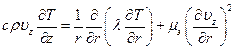 (6.27)
(6.27)
Уравнение вязкости:
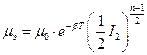
Уравнение расхода:
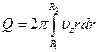
ГУ:
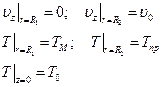
Обезразмерим уравнение (6.26), для этого определим характерную температуру, размеры и скорость (u0, T0, R1):
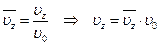 , где
, где 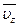 -безразмерная скорость
-безразмерная скорость
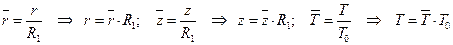
Разделим уравнение (6.26) на r:
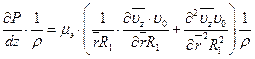
В дальнейшем при выводе знак штриха для простоты опустим, т.е. 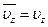 .
.
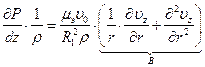 (6.28)
(6.28)
Умножим обе части уравнения (6.28) на 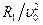 , получим:
, получим:
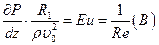 , где (6.29)
, где (6.29)
Eu – критерий Эйлера;
Re – критерий Рейнольдса. Для полимеров, у которых значение вязкости велико, обычно 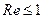 . Для воды и невязких сред
. Для воды и невязких сред 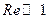 .
.
Уравнение (6.29) – это безразмерное уравнение движения, в котором критерий Рейнольдса выражает соотношение сил инерции к силам вязкости:
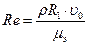
Критерий Эйлера выражает соотношение сил давления и сил инерции.
Обезразмерим уравнение (6.27):
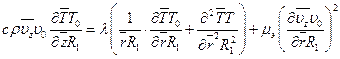 (6.30)
(6.30)
Штрихи опустим, разделим обе части уравнения (6.30) на 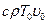 и умножим на
и умножим на 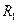 , получим:
, получим:
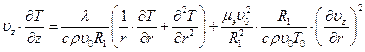
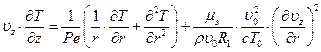
 , где (6.31)
, где (6.31)
Ek – критерий Эккета, 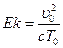 , показывает соотношение между кинетической и тепловой энергией;
, показывает соотношение между кинетической и тепловой энергией;
Pe – критерий Пекле, 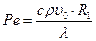 , соотношение тепла, переносимого конвекцией и тепла, переносимого теплопроводностью, для полимеров
, соотношение тепла, переносимого конвекцией и тепла, переносимого теплопроводностью, для полимеров 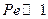 .
.
Уравнение (6.29) и (6.31) – общая постановка задачи для течения в кабельной головке в безразмерном виде.
Используя МКР, задача решается с использованием следующей разностной схемы: (6.32) и (6.33)
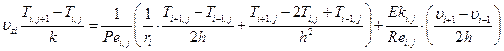 (6.32)
(6.32)
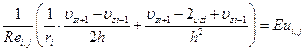 (6.33)
(6.33)
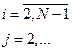
ГУ:
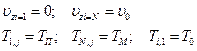
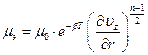
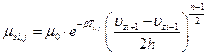
Алгоритм расчета:
1. В первом сечении по длине, используя начальное распределение температуры, рассчитываются поля температур и скоростей по уравнениям (6.32) и (6.33).
2. Вычисленные поля температур и скоростей используются для перевычисления критериев подобия.
3. С новыми значениями критериев вновь рассчитываются поля скоростей и температур и проводятся сравнения по температуре или по скорости (или по вязкости) на ближайших итерациях:
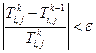 (6.34)
(6.34)
Если условие (6.34) выполняется, то переходят к расчету на следующем сечении. В противном случае расчет повторяют вновь.
 2014-02-12
2014-02-12 557
557








