Волгодонск

УДК 681.3 (075.8)

Рецензент д.т.н., профессор В.В. Кривин

Составитель ст. преп. Цуверкалова О.Ф.

Методические указания содержат курс лекций по дисциплине «Дискретная математика» /ВИТИ НИЯУ МИФИ. Волгодонск, 2010. 117 с.

Предназначены для студентов очной, очно-заочной и заочной формы обучения специальности 230201 – Информационные системы и технологии, 220301 – Автоматизация технологических процессов и производств

ã ВИТИ НИЯУ МИФИ, 2010

ã О.Ф. Цуверкалова, 2010

1. алгебра МНОЖЕСТВ

1.1. Понятие множества. Обозначение принадлежности

Математическое понятие множества постепенно выде­лилось из привычных представлений о совокупности, соб­рании, классе, семействе и т. д. В 1872 г. Георг Кан­тор, создатель теории множеств, определил множество как «объединение в одно целое объектов, хорошо разли­чаемых нашей интуицией или нашей мыслью». В первом издании «Теории множеств» Бурбаки, поя­вившемся в 1939 г., в сводке результатов можно найти следующее предложение: «Множество образуется из элементов, обладающих некоторыми свойствами и на­ходящихся в некоторых отношениях между собой или с элементами других множеств».

Объекты, сущности или элементы, составляющие мно­жество, обозначаются строчными латинскими буквами: х, а,...; множество часто обозначают прописными ла­тинскими буквами Е, N,.... Знак Î обозначает вхож­дение или принадлежность; х Î Е читается: «элемент х принадлежит множеству Е», или короче: «х— элемент множества Е». Следует различать «общий элемент» х множества Е, т. е. произвольный элемент, характеризую­щийся единственным свойством «принадлежать множест­ву», и конкретные элементы а, b, c,..., каждый из ко­торых отличен от остальных. Если х не принадлежит Е, будем писать х Ï Е, что читается «х не является элемен­том множества Е» или «х не принадлежит множеству Е». Если множество содержит конечное число элементов, говорят, что оно конечно; в противном случае множест­во называется бесконечным. Множество Е, состоящее из элементов а, b,..., записывается

Е= {а. b........}.

Примеры. 1) Множество четных цифр Р={2, 4,6,8}.

2) Множество трехзначных чисел в двоич­ной системе:

В₃ = {000, 001, 010, 011, 100, 101, 110, 111}.

1.2. Способы задания множеств

1) Множество может быть задано перечислением всех его элементов.

Пример. Множество цифр: {0,1,..., 9}.

2) Обобщение первого способа состоит в том, что каждый элемент задаваемого множества определяется по некоторому элементу уже известного множества.

Пример. Считая известным множество целых чисел

Z = {....-3.-2,-1, 0. 1, 2, 3,...},

определим множество степеней числа 2

{…, 2^-3, 2^-2, 2^-1, 2⁰, 2¹, 2², 2³, …}

3) Другой способ задания множеств — описание огра­ничительного свойства, выделяющего элементы множе­ства Е среди элементов более широкого, или основного (универсального, универсума), множества U. Множество Е называется частью, или под­множеством множества U.

Пример. Пусть дано множество N натуральных чисел N = {1, 2, 3,...}. Рассмотрим совокупность всех тех элементов этого мно­жества, которые делятся на 2 (ограничительное и харак­теризующее свойство); полученное множество есть мно­жество четных чисел Р={2, 4, 6,...}.

4) В дальнейшем мы увидим также, что новые мно­жества задаются при помощи некоторых операций над множествами.

1.3. Множество подмножеств. Включение

Пусть U — основное множество. Основное, или фунда­ментальное, множество в математике может быть образо­вано всеми элементами какого-нибудь определенного типа.

Пример. Множество прямых плоскости, множество простых чисел и т. д.

Два свойства, эквивалентные относительно основного множества, определяют одну и ту же часть этого мно­жества, и обратно. Множество элементов U, облада­ющих свойством хÎ Е, очевидно, совпадает с Е.

Пример. Пусть I — множество нечетных чисел в де­сятичной системе

I = {1, 3, 5, 7, 9, 11, 13. 15, 17, 19....};

за основное множество примем множество N натураль­ных чисел. Можно определить множество нечетных чи­сел исходя из свойства оканчиваться на нечетную деся­тичную цифру 1, 3, 5, 7 или 9 (Р ₁); то же множество соответствует свойству не делиться на 2 (Р ₂). Свойства P₁ и P₂ эквивалентны относительно N и задают мно­жество нечетных чисел, подмножество основного множе­ства N.

Обратимся теперь к свойству не быть целым числом (Р ₃), соответствующее этому свойству подмножество ос­новного множества N не содержит ни одного элемента; такое множество будем называть пустым и обозначать Æ.

Таким образом, свойства, присущие некоторым эле­ментам множества U, могут служить для задания под­множеств этого множества; свойство, отличное от всех свойств элементов U, порождает пустое множество, пус­тое подмножество множества U. Напротив, наибольшее подмножество, т. е. само множество U, может быть за­дано любым свойством, присущим всем элементам основ­ного множества.

Пусть А и В - два подмножества основного множест­ва U. Если все элементы из А принадлежат В, то гово­рят, что А содержится (или включено) в В; употреб­ляются также выражения; В содержит A, или А есть часть множества В. В этом случае будем писать А Ì В или В É A.

Пример. Множество Р четных чисел содержится в множестве N натуральных чисел: РÌN.

При задании множества путем перечисления элемен­тов или установления соответствия с элементами ранее изученного множества, мы можем сформулировать харак­теристические свойства общего элемента подмножества Е основного множества U; эти формулировки будут теоремами, требующими доказательства; способ задания Е — аналитический.

Наоборот, если мы знаем характеристические свойст­ва общего элемента подмножества Е, то мы можем определить, какие элементы основного множества U принадлежат этому подмножеству: речь идет о пара­метризации подмножества Е: такой способ задания яв­ляется синтетическим.

Из соотношений А Ì В и В Ì С следует соотношение A Ì С; следовательно, отношение включения транзитивно. Заметим, что из А Ì В и B Ì A следует А = В, и наоборот. Действительно, два множества равны (идентичны), если они состоят из одних и тех же эле­ментов.

Иногда вво­дят понятия собственного и несобственного подмноже­ства. Множество B называется собственным подмножеством множества A, если оно отлично от A и от .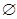

В этом случае пишут A Í B, если возможен случай A = B (в этом случае A называется несобственным подмноже­ством множества В), и А Ì В, если В содержит хотя бы один элемент, не принадлежащий A. При такой системе обозначений невозможен случай, когда А Ì В и B Ì A одновременно.

Свойства подмножеств:

1) Пустое множество является подмножеством любого множества: 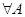Æ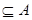

2) Всякое множество является своим собственным подмножеством: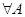

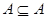
Два множества называются равными, если они содержат одни и те же элементы и количество этих элементов одинаково.

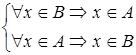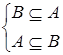или или .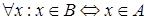

Множеством подмножеств некоторого основного или произвольного множества Е называется множество, эле­ментами которого являются подмножества множества Е. Это множество P(Е) включает в качестве элементов пустое множество 0 и само множество Е; каждый от­дельный элемент Е есть также подмножество множест­ва Е.

Пример. Е ={ а, b, с};

P(Е)={{Æ}, {а}, {b}, {с}, {а, b}, {а, с}, {b, с}, {а, b, с,}}.

Теорема: Конечное множество, содержащее n элементов, имеет 2 ⁿ подмножеств.

Доказательство: Пусть 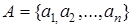и пусть BÍA. Поставим ему в соответствие набор длины n из 0 и 1, устроенный так: если элемент a_i Î B, то на i -ом месте ставим 1, в противном случае - 0.

A:				…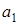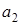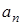
		¯	¯		¯
В:				…

Каждому подмножеству множества А соответствует свой набор. И наоборот, по всякому набору нулей и единиц можно выписать множество, являющееся подмножеством А. Таким образом, между всеми подмножествами A и п -местными наборами 0 и 1 существует взаимно однозначное соответствие, т.е. подмножеств столько же, сколько таких наборов. Поскольку на каждое из п мест можно поставить либо 0, либо 1, то общее количество п -местных наборов равно 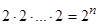, а следовательно, и подмножеств 2 ⁿ.