Поле комплексных чисел

Комплексное число 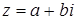,где 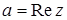- действительная часть и 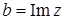- мнимая часть, можно рассматривать как упорядоченную пару
(а, b) двух действи­тельных чисел, которые являются элементами множества R.

На множестве комплексных чисел определяются два внутрен­них закона - сложение и умножение:

; .

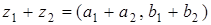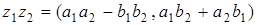Два числа z₁ и z₂ равны, если a₁ = a₂ и b₁ = b₂.

В принятых обозначениях i = (0,1), следовательно, i² = (0,1)(0,1) = (-1,0) или i² = -1. Действия над комплексными числами в форме 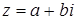можно выполнять как с действитель­ными числами, заменяя всякий раз i² на -1.

Числом, комплексно-сопряженным с числом г = а + bi, является число 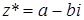. Справедливы следующие соотношения:

.

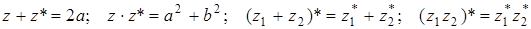Множество комплексных чисел составляет коммутативную группу относительно сложения. Действительно, сложение комму­тативно и ассоциативно, нейтральным элементом служит нуль (0, 0), а симметричное числу 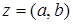есть .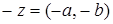

Относительно умножения нейтральным элементом является единица (1, 0), и всякое отличное от нуля комплексное число 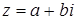имеет симметричное (обратное)

,

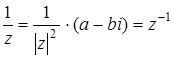где - модуль комплексного числа. Т.к. умноже­ние дистрибутивно относительно сложения, то множество комплекс­ных чисел составляет поле.

Указанное представление называется представлением комплексного числа в алгебраической форме. Комплексное число представляется также в тригонометрической и экспоненциальной форме:

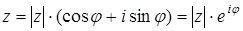
Здесь 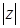- модуль и j - аргумент комплексного числа, определяемый с точностью до целого кратного 2π, причем .

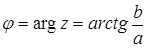Указанное представление удобно для вычисления произведения двух комплексных чисел:

.

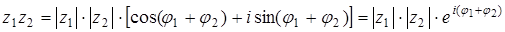Таким образом, 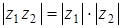и .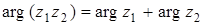

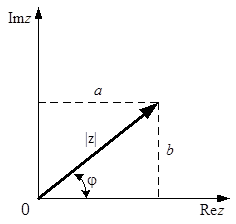
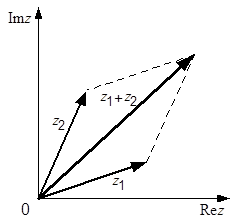
Геометрически представление комплексных чисел представлено на рис. 7.1а. Суммированию комплексных чисел соответствует геометрическое сложение векторов на комп­лексной плоскости (рис. 7.1б). Отсюда, в частности, следует 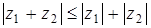(правило треугольника).

а)	б)
Рис. 7.1. Геометрическое представление комплексных чисел