Рассмотрим множество многочленов (полиномов) от переменной х над числовым полем Р, т. е. выражения вида 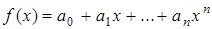 , где п - целое неотрицательное число, а коэффициенты многочлена а 0, а 1,…, ап - числа из поля Р (действительные или комплексные). Наибольшее число п, при котором ап ¹ 0, называется степенью многочлена и обозначается deg f(x). Два многочлена
, где п - целое неотрицательное число, а коэффициенты многочлена а 0, а 1,…, ап - числа из поля Р (действительные или комплексные). Наибольшее число п, при котором ап ¹ 0, называется степенью многочлена и обозначается deg f(x). Два многочлена 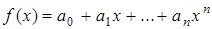 и
и 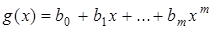 тождественно равны, если п = т и
тождественно равны, если п = т и 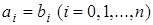 . Определим на множестве многочленов два внутренних закона - аддитивный и мультипликативный.
. Определим на множестве многочленов два внутренних закона - аддитивный и мультипликативный.
Сумма двух многочленов f (x) + g (x) - это многочлен, у которого коэффициент при каждой степени переменного х равен сумме коэффициентов многочленов f (x) и g (x) при той же степени х. Если степени складываемых многочленов не равны, то многочлен меньшей степени дополняется до старшей степени членами с нулевыми коэффициентами. При этом
deg [ f (x) + g (x)] £ max [deg f (x), deg g (x)].
Поскольку операция сложения многочленов определяется через сложение его коэффициентов, а сложение чисел ассоциативно и коммутативно, то операция сложения многочленов также ассоциативна и коммутативна. Нейтральным элементом относительно сложения является многочлен, все коэффициенты которого нули. Всякий многочлен f (x) обладает симметричным ему, все коэффициенты которого противоположны коэффициентам f (x), т. е. 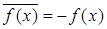 . Следовательно, множество многочленов является абелевой группой относительно сложения.
. Следовательно, множество многочленов является абелевой группой относительно сложения.
Произведение двух многочленов определяется как многочлен f (x) g (x), получающийся умножением каждого члена многочлена f (x) на каждый член многочлена g (x), суммированием полученных произведений и приведением подобных членов. Очевидно,
deg [ f (x) g (x)] = deg f (x) + deg g (x).
Операция умножения многочленов ассоциативна, коммутативна и дистрибутивна относительно сложения. Нейтральным элементом относительно умножения служит многочлен, у которого а 0 = 1, а все остальные коэффициенты равны нулю. Коммутативность и ассоциативность умножения доказывается аналогично сложению.
Таким образом, множество многочленов есть коммутативное кольцо. Это кольцо также унитарно (кольцо с единицей). Можно показать, что множество многочленов не имеет делителей нуля, следовательно, оно есть кольцо целостности.
Любой многочлен можно единственным образом представить в виде 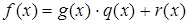 ,
,
где 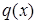 - частное от деления f (x) на g (x), а
- частное от деления f (x) на g (x), а 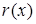 - остаток. При этом deg r (x) < deg g (x), а также, если deg f (x) ³ deg g (x), то
- остаток. При этом deg r (x) < deg g (x), а также, если deg f (x) ³ deg g (x), то
deg q (x) = deg f (x) - deg g (x).
Число λ называют нулем многочлена f (x),если f (l) =0. Говорят также, что l есть корень уравнения f (х) = 0. Для того чтобы l был нулем многочленf f (x), необходимо и достаточно, чтобы этот многочлен делился без остатка на х- l. Если многочлен f (x) делится без остатка на (х- l) s, где s - наибольшее натуральное число, для которого такое деление возможно, то l называется нулем кратности s. Нуль кратности единица называется простым.
Основная теорема алгебры утверждает, что многочлен п -й степени с действительными коэффициентами имеет не более п различных действительных нулей. Если многочлен рассматривается над полем комплексных чисел, то с учетом кратности корней их общее число всегда равно п.
 2014-02-12
2014-02-12 1746
1746








