Из таблицы 9.1 видно, что между функциями имеется зависимость:
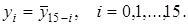
Из этих зависимостей следует, что любая функция двух переменных (включая константы) выражается в аналитической форме через совокупность шести функций, содержащей отрицание 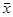 и любую из каждой пары функций
и любую из каждой пары функций 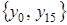 ,
, 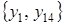 ,
, 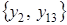 ,
, 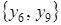 ,
, 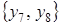 . Например, такой совокупностью могут служить функции: константа 0, отрицание
. Например, такой совокупностью могут служить функции: константа 0, отрицание 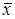 , конъюнкция
, конъюнкция 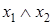 , дизъюнкция
, дизъюнкция 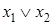 , эквиваленция
, эквиваленция 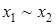 и импликация
и импликация 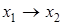 . Эта совокупность функций используется в исчислении высказываний.
. Эта совокупность функций используется в исчислении высказываний.
Выбранная таким способом совокупность шести функций является избыточной. Можно показать, что импликация и эквиваленция выражаются через остальные функции этой совокупности:
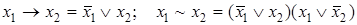
Для этого достаточно построить таблицу соответствия и сравнить ее с табл. 9.1:

Таким образом, комплект элементарных функций сокращается до четырех: константа 0, отрицание 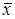 , конъюнкция
, конъюнкция 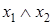 , дизъюнкция
, дизъюнкция 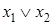 . Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Далее будет показано, что любые булевы функции могут быть выражены через отрицание и конъюнкцию или через отрицание и дизъюнкцию.
. Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Далее будет показано, что любые булевы функции могут быть выражены через отрицание и конъюнкцию или через отрицание и дизъюнкцию.
Более того, для записи любой булевой функции достаточно только одной из двух элементарных функций - стрелки Пирса или штриха Шеффера. Это вытекает из следующих соотношений (их доказательство приводится аналогично с помощью таблиц соответствия):
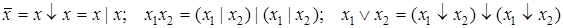
 2014-02-12
2014-02-12 1132
1132








