Нормированные пространства

Пусть L - линейное пространство. Функция р, определенная на L, называется нормой, если она удовлетворяет следующим трем условиям:

1) р(х) ³ 0, причем р(х) = 0 только при х = 0,

2) p(x + y) £ p(x) + p(y), x,y Î L.

3) р(ax) = \a\ р(х), каково бы ни было число a.

Линейное пространство L, в котором за­дана некоторая норма, мы назовем нормированным простран­ством. Норму элемента x Î L мы будем обозначать симво­лом .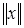

Всякое нормированное пространство становится метрическим пространством, если ввести в нем расстояние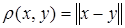

Справедливость аксиом метрического пространства тотчас же вытекает из свойств нормы. На нормированные про­странства переносятся, таким образом, все те понятия и факты, которые справедливы для метрических пространств.

Рассмотрим примеры нормированных пространств. Многие из пространств, рассматривавшихся в качестве примеров метрических пространств, в действительности могут быть наделены естественной структу­рой нормированного пространства.

1. Прямая линия R ¹ становится нормированным пространством, если для всякого числа х Î R ¹ положить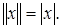

2. Если в действительном п -мерном пространстве R ⁿ с элементами 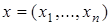положить

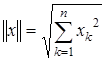
то все аксиомы нормы будут выполнены. Формула

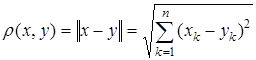
определяет в R ⁿ ту самую метрику, которую мы в этом про­странстве уже рассматривали.

В этом же линейном пространстве можно ввести норму

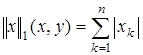
или норму

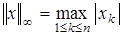
Эти нормы определяют в R ⁿ метрики, которые мы рассматри­вали в примерах 4 и 5 п. 1. Проверка того, что в ка­ждом из этих случаев аксиомы нормы действительно выполнены, не составляет труда.

3. В пространстве С [a, b] непрерывных функцийна отрезке [a, b] определим норму формулой

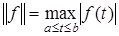
Соответствующая метрика уже рассматривалась в примере 6 п. 1.