Типы булевых функций

В алгебре логики из множества 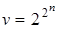различных булевых функций п переменных у= f( 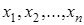) выделяются следующие пять типов булевых функций.

1) Функции, сохраняющие константу 0, т. е. такие f( 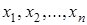), что f (0,…,0) = 0. Так как на одном из 2 ^п наборов ( 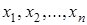) значения таких функций фиксированы, то их число равно 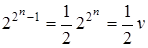, т. е. половина всех функций п переменных сохраняет константу 0.

2) Функции, сохраняющие константу 1, т. е. такие f( 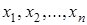), что f (1,…,1) = 1. Их число, как и в предыдущем случае, равно половине общего числа всех функций п переменных.

3) Самодвойственные функции, т. е. такие, которые принимают противоположные значения на любых двух противоположных наборах. Если в общей таблице соответствия наборы, как обычно следуют в порядкеих номеров, то противоположные друг другу наборы располагаются симметрично относительно середины их рас­положения. Это значит, что строка значений самодвойственной функ­ции должна быть антисимметричной относительно своей середины. Самодвойственная функция полностью определяется заданиемее значений на половине всех наборов (остальные значения определя­ются по условию антисимметричности), поэтому число независимых наборов равно 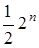и число всех таких функций .

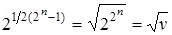4) Линейные функции, т. е. такие, которые представляются в алгебре Жегалкина каноническим многочленом, не содержащим произведений переменных: 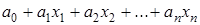, где коэффи­циенты 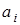принимают значения 0 или 1. Так как всего коэффициентов п +1, то число различных линейных многочленов будет 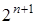. В силу однозначности представления функции канони­ческим многочленом это число выражает и количество линейных функций.

5) Монотонные функции, т.е. такие, которые для любых двух наборов из множества значений переменных, частично упорядочен­ного соотношением (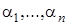) £ () 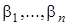при 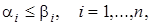, удовлетворяют неравенству
f (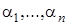) £ f ().

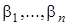Рассмотренные типы функций замкнуты относительно операции суперпозиции, т. е. суперпозиция любого числа булевых функций данного типа является функцией того же типа.