Канонические многочлены

Любая булева функция приводится к каноническому многочлену, члены которого не содержит числовых коэффициентов и линейны относительно любой из переменных (переменные входят только в первой степени).

Действительно, если привести данную функцию к совершенной нормальной форме и заменить все дизъюнкции через суммы по модулю 2, а отрицание переменных представить в соответствии с тождеством 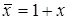, то после раскрытия скобок получим некоторое алгебраическое выражение. Оно приводится к канониче­скому многочлену на основе соотношений х + х = 0 и хх = х. Такое представление всегда возможно и единственно (с точностью до по­рядка расположения членов).

Пример.

(1 + х + у) (1 + ху) + (х + ху) у = 1 + х + у + ху + хху + уху + ху + хуу =

= 1 + х + у + ху + ху + ху + ху + + ху = 1 + х + у + ху.

Проблема разрешимости в алгебре Жегалкина сводится к ука­занным преобразованиям, в процессе которых делается вывод о вы­полнимости той или иной формулы.

Пример.

х(х ® у) ® у = х (1 + х + ху) ® у = ху ® у = 1 + ху + хуу =1 + ху + ху = 1

Так как эта формула является тождественной единицей, то она невыполнима.

Преимущество алгебры Жегалкина состоит в арифметизации логики, что позволяет выполнять преобразования булевых функций, используя опыт преобразования обычных алгебраических выраже­ний. Ее недостаток по сравнению с булевой алгеброй - сложность формул, что особенно сказывается при значительном числе перемен­ных, например:

х Ú у Ú z = х + у + z + ху + хz + уz + хуz.

Однако при использовании вычислительных машин различия в сложности выполнения операций булевой алгебры и арифметиче­ских операций значительно ослабляются.