Другая замечательная алгебра булевых функций строится на основе операций сложения по модулю 2 и конъюнкции. Она называется алгеброй Жегалкина по имени предложившего ее советского ученого. Непосредственной проверкой по таблицам соответствия устанавливаются следующие основные свойства этой алгебры:
- коммутативность х + у = у + х; ху = ух;
- ассоциативность х + (у + z) = (х + у) + z; х(уz) = (ху)z;
- дистрибутивность умножения относительно сложения х(у + z) = ху + хz;
- свойства констант. 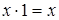 ;
; 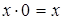 ;
; 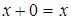
Все эти свойства подобны обычной алгебре, но в отличие от булевой алгебры закон дистрибутивности сложения относительно умножения не имеет силы. Справедливы также следующие тождества:
- закон приведения подобных членов при сложении х + х =0;
- закон идемпотентности для умножения хх = х.
Таким образом, в формулах алгебры Жегалкина, как и в булевой алгебре, не могут появляться коэффициенты при переменных и показатели степени. С помощью табл. 9.1 выводятся также следующие соотношения:
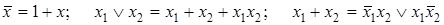
Первые два тождества позволяют перейти от любой формулы булевой алгебры к соответствующей ей формуле алгебры Жегалкина, а с помощью третьего тождества осуществляется обратный переход.
Пример.
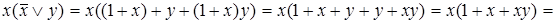
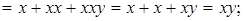
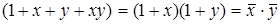
Через операции алгебры Жегалкина можно выразить все другие булевы функции:
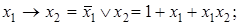
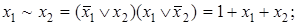
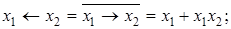
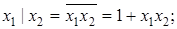
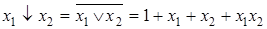 .
.
 2014-02-12
2014-02-12 1474
1474
