Конституенты и представление функций

Проблема разрешимости

Формула(или соответствующаяей функция) называется выполнимой, если она не является тождест­венным нулем или единицей. Решение с помощью конечного числа действий вопроса, является ли данная формула выполнимой, т. е. не равна ли она тождественно нулю или единице, носит назва­ние проблемы разрешимости.

Ответ на этот вопрос можно получить, построив для данной формулы таблицу соответствия, что сводится по существу к опре­делению значений формулы при всевозможных наборах значении входящих в нее переменных. Если на всех наборах формула прини­мает значения только 0 или только 1, то она невыполнима.

При большом количестве переменных такой способ практически неосуществим из-за огромного числа возможных наборов значений переменных. Более удобный путь - приведение формулы к нор­мальной форме. Если в процессе такого приведения формула не обращается в тождественный 0 или 1, то это свидетельствует о ее выполнимости.

Для совокупности переменных 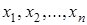выражение 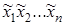называют конституентой единицы, а выражение 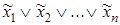- конституентой нуля ( 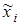означает либо 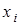, либо 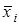). Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствую­щем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания - нулю (единице). Например, конституенте единицы 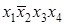соот­ветствует набор (1011), а конституенте нуля 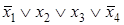- набор (1001).

Так как совершенная дизъюнктивная (конъюнктивная) нор­мальная форма является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f( 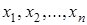) обращается в единицу (нуль) только при наборах значений переменных 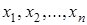, соответствующих этим конституентам. На остальных наборах эта функция обращается в нуль (единицу).

Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей. Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам зна­чений переменных, на которых функция принимает значение, рав­ное единице (нулю).

Пример. Функции, заданной таблицей

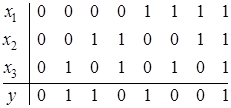
соответствуют совершенные нормальные формы:

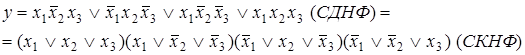
Полученные выражения можно преобразовать к другому видуна основании свойств булевой алгебры.