Свойство безотказности восстанавливаемых изделий характеризуется средним числом отказов 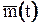 за время t
за время t
 ,
,
где N – число испытываемых изделий;  число отказов изделия за время t.
число отказов изделия за время t.
В соответствии с двумя способами задания потока отказов для восстанавливаемых систем применяют различные показатели безотказности.
1. При задании потока отказов как дискретного случайного процесса 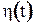 на интервале (0;t) показателем безотказности является параметр потока отказов
на интервале (0;t) показателем безотказности является параметр потока отказов  среднее число отказов, ожидаемых в малом интервале времени; η(t) – числа отказов на интервале (0;t):
среднее число отказов, ожидаемых в малом интервале времени; η(t) – числа отказов на интервале (0;t):
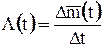 ,
,
где 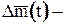 приращение среднего числа отказов за время Δt, т.е. среднее число отказов от момента t до момента t + Δt.
приращение среднего числа отказов за время Δt, т.е. среднее число отказов от момента t до момента t + Δt.
В вероятностной трактовке параметр потока отказов  представляет собой производную
представляет собой производную
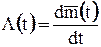
Вывод: параметр потока отказов – отношение числа отказов системы на некотором малом отрезке времени к значению этого отрезка.
2. При задании потока отказов как последовательности случайных наработок между отказами 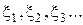 показателем безотказности является средняя наработка на отказ
показателем безотказности является средняя наработка на отказ 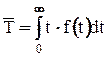 .
.
Предполагается, что наработки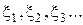 имеют одинаковую плотность распределения f(t)).
имеют одинаковую плотность распределения f(t)).
Для статистического определения средней наработки на отказ 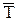 испытываются
испытываются 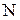 одинаковых восстанавливаемых систем. Полагается, что каждая из этих систем проработала в течение времени
одинаковых восстанавливаемых систем. Полагается, что каждая из этих систем проработала в течение времени 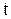 .
.
Тогда средняя наработка на отказ 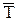 определяется из выражения
определяется из выражения
 ,
,
где 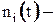 число отказов
число отказов 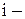 ой системы на интервале (0;t).
ой системы на интервале (0;t).
Средняя наработка на отказ 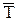 и параметр потока отказов Λ связаны соотношением
и параметр потока отказов Λ связаны соотношением 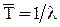 .
.
При длительной наработке t, значительно большей среднего значения 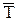
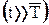 параметр потока отказов Λ(t) восстанавливаемой системы возрастает, затем начинаются колебания, затухающие на уровне
параметр потока отказов Λ(t) восстанавливаемой системы возрастает, затем начинаются колебания, затухающие на уровне  .
.
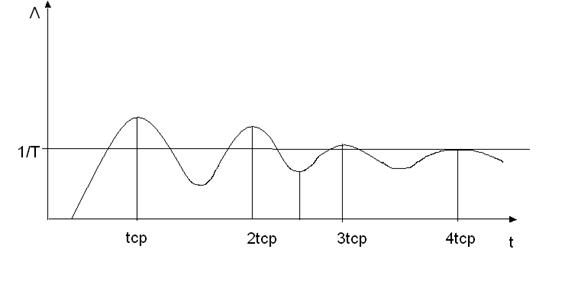
Наблюдаемые максимумы Λ(t) соответствуют средней наработке до отказа первого, второго, третьего поколений и т.д.
В сложных изделиях параметр потока отказов рассматривается как сумма параметров потоков отказов. Составляющие потоки можно рассматривать по узлам или по типам устройств: 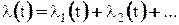
Средняя наработка между отказами 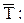
 .
.
 2014-02-12
2014-02-12 846
846








