2014-02-12
4204
ЛЕКЦИЯ 9
Этот метод основан на использовании формулы полной вероятности.
В сложной системе выделяется особый элемент, все возможные состояния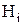 
которого образуют полную группу событий: 
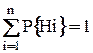. Если анализируемая система находится в состоянии 
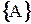, то вероятность этого состояния 
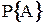определяется выражением
.
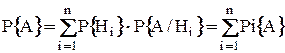Второй сомножитель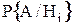 
определяет вероятность состояния 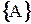при условии, что особый элемент находится в состоянии .
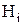Рассмотрение 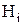- го состояния особого элемента как безусловного позволяет упростить структурную схему надежности системы и свести ее к последовательно-параллельному соединению элементов.
Рассмотрим мостиковую структурную схему надежности.
 |
а б
В этой схеме элемент 5 выделяется как особый с двумя возможными состояниями: 1 – наличие цепи между точками «а» и «б»; 2 – отсутствие цепи между точками «а» и «б». Поэтому можно перейти от мостиковой схемы к двум структурным схемам, соответствующим состояниям «1» и «2»:
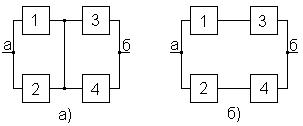
«а» - работоспособное состояние;
|
|
|
«б» - неработоспособное состояние
В данном случае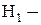 
работоспособное состояние элемента «5» с вероятностью 
; 
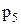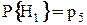(рисунок «а»);
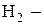неработоспособное состояние элемента «5» с вероятностью отказа 
;
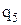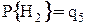(рисунок «б»).
Если состояние 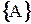– наличие цепи между точками «а» и «б», то вероятност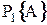и 
и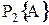 
нахождения системы в состояниях «1» и «2» соответственно определяются из исходного выражения
.
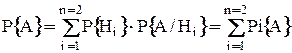Следовательно, имеем:
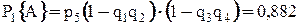– (схема «а»);
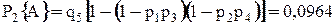– (схема «б»);
;
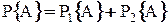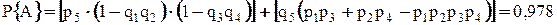
Таким образом, оценка безотказности снизу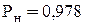 
по методу миимальных путей и сечений совпадает с фактической безотказностью системы 
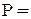0,978, рассчитанной методами перебора состояний и разложения относительно особого элемента 
.
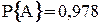Сопоставление обоих методов расчета надежности показывает, что выделение особого элемента с последующим анализом упрощенных структурных схем существенно сокращает объем расчетных работ.
