ЛЕКЦИЯ 7
А б
Для всех элементов структурной схемы известны вероятности безотказной работы Р1 Р2 Р3 Р4 Р5 и соответствующие им вероятности отказа (обрыв) q1 q2 q3 q4 q5. Необходимо определить вероятность наличия цепи между точками «а» и «в».
Существует несколько методов расчета надежности систем со сложной структурой.
Метод перебора состояний, основанный на теории множеств, применяется в случаях, когда структурная схема надежности не содержит только последовательно-параллельное соединение элементов.
В качестве примера рассмотрим мостовую схему надежности.
 |
а б
Для всех элементов данной структурной схемы известны вероятности безотказной работы p1, p2, p3, p4, p5 и соответствующие им вероятности отказа (обрыв цепи) q1 q2 q3 q4 q5. При этом все элементы приняты равнонадежными: вероятность безотказной работы 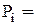 0,9; вероятность отказа
0,9; вероятность отказа 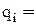 0,1.
0,1.
Определить вероятность наличия цепи между точками «а» и «в».
Сущность метода состоит в определении двух непересекающихсямножеств состояний элементов, соответствующих работоспособному и неработоспособному состояниям системы. Каждое из этих состояний характеризуется набором элементов, находящихся в работоспособном и неработоспособном состояниях.
Известно, что при независимых отказах вероятность каждого из состояний определяется произведением вероятностей нахождения элементов в соответствующих состояниях. Тогда при числе состояний равном 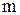 , вероятность работоспособного состояния системы
, вероятность работоспособного состояния системы 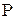 и вероятность отказа
и вероятность отказа 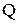 определяется выражениями
определяется выражениями
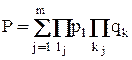 ;
; 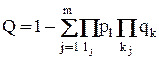 .
.
Здесь m – общее число работоспособных состояний в каждом j-том состоянии;
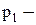 вероятность исправного состояния
вероятность исправного состояния 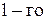 элемента;
элемента;
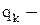 вероятность неисправного состояния
вероятность неисправного состояния 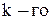 элемента;
элемента;
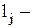 число исправных элементов;
число исправных элементов;
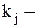 число неисправных элементов.
число неисправных элементов.
Расчет надежности с использованием метода перебора состояний удобно представлять в виде таблицы, в которой введены следующие обозначения:
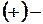 работоспособное состояние элемента;
работоспособное состояние элемента;
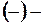 неработоспособное состояние элемента.
неработоспособное состояние элемента.
Таблица перебора состояний для мостиковой схемы
| № состояния | Состояние элементов | Вероятность состояния | |||||
| 1. | + | + | + | + | + | Р1 Р2 Р3 Р4 Р5 = 0.95 | |
| 2. | - | + | + | + | + | Р2 Р3 Р4 Р5 q1 |  = 0.1*0.94 = 0.1*0.94 |
| 3. | + | - | + | + | + | Р1 Р3 Р4 Р5 q2 | |
| 4. | + | + | - | + | + | Р1 Р2 Р4 Р5 q3 | |
| 5. | + | + | + | - | + | Р1 Р2 Р3 Р5 q4 | |
| 6. | + | + | + | + | - | Р1 Р2 Р3 Р4 q5 | |
| 7. | - | + | - | + | + | Р2 Р4 Р5 q1 q3 | 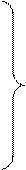 0.12*0.93 0.12*0.93 |
| 8. | - | + | + | - | + | Р2 Р3 Р5 q1 q4 | |
| 9. | - | + | + | + | - | Р2 Р3 Р4 q1 q5 | |
| 10. | + | - | - | + | + | Р1 Р4 Р5 q2 q3 | |
| 11. | + | - | + | - | + | Р1 Р3 Р5 q2 q4 | |
| 12. | + | - | + | + | - | Р1 Р3 Р4 q2 q5 | |
| 13. | + | + | - | + | - | Р1 Р2 Р q3 q5 | |
| 14. | + | + | + | - | - | Р1 Р2 Р3 q4 q5 | |
| 15. | - | + | - | + | - | Р2 Р5 q1 q3 q5 | 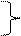 = 0.13*0.92 = 0.13*0.92 |
| 16. | + | - | + | - | - | Р1 Р3 q2 q4 q5 |
При принятых исходных данных вероятность работоспособного состояния системы:
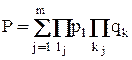
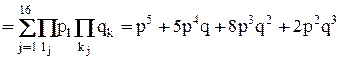
Подставляя числовые значения, получаем 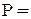 0,978.
0,978.
При сравнительно простой структурной схеме надежности применение метода перебора состояний сопряжено с громоздкими выкладками и вычислениями. Однако применение современных компьютерных технологий устраняет данное ограничение.
 2014-02-12
2014-02-12 3115
3115
