С постоянным резервом
Расчет надежности невосстанавливаемых систем
ЛЕКЦИЯ 11
При общем постоянном резервировании структурная схема надежности системы включает параллельно соединенные элементы.
Как отмечалось ранее, кратность резервирования 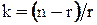 , где n - общее число однотипных элементов; r - число элементов необходимых для функционирования системы. Значение параметра «
, где n - общее число однотипных элементов; r - число элементов необходимых для функционирования системы. Значение параметра «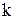 » может быть целым числом (если
» может быть целым числом (если 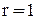 ) или дробным числом (если
) или дробным числом (если 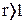 ).
).
Для «m» параллельно работающих элементов при r = 1 кратность резервирования 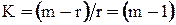 . Следовательно,
. Следовательно, 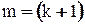 .
.
Вероятность отказа резервированной системы 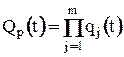 .
.
Для равнонадежных элементов 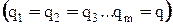 вероятность отказа
вероятность отказа 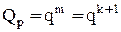 .
.
Снижение вероятности отказа за счет резервирования (эффективность резервирования):
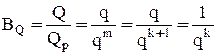 .
.
Данная зависимость показывает, что чем меньше вероятность отказа каждого из элементов, тем выше эффективность постоянного резервирования.
Пример: 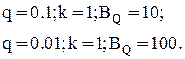
Рассмотрим связь показателей надежности группы резервированных элементов, кратности резервирования и длительности работы элементов при экспоненциальномзаконе распределения времени их безотказной работы.
Если интенсивность отказов каждого из элементов равна 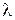 , то получим:
, то получим:
вероятность отказа:
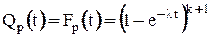 ;
;
вероятность безотказной работы:
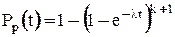 ;
;
плотность функции распределения вероятности отказа:
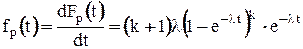 .
.
Интенсивность отказов всей системы:
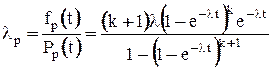 .
.
Анализ этой зависимости показывает:

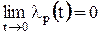 ;
; 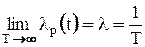 ,
,
где 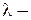 поток отказов отдельного элемента;
поток отказов отдельного элемента; 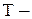 среднее время наработки до отказа отдельного элемента.
среднее время наработки до отказа отдельного элемента.
Графики зависимости параметров 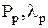 от кратности резервирования:
от кратности резервирования:
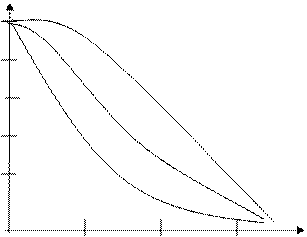 Pp (t/T) 0,8 к=4 0,6 к=1 0,4 0,2 к=0 1 2 3 t/T Pp (t/T) 0,8 к=4 0,6 к=1 0,4 0,2 к=0 1 2 3 t/T | λp/λ 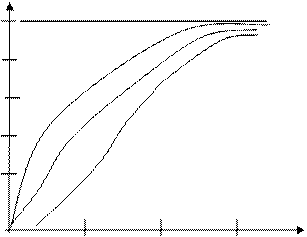 к=0 0,8 к=1 0,6 к=4 0,4 к=2 0,2 1 2 3 t/T к=0 0,8 к=1 0,6 к=4 0,4 к=2 0,2 1 2 3 t/T |
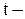 время работы системы.
время работы системы.
Графики показывают, что постоянное резервирование эффективно на начальном участке работы системы, когда 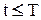 .
.
Для группы резервированных элементов средняя наработка до отказа:
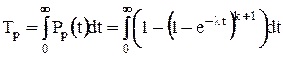 .
.
Полагаем: 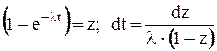 .
.
После подстановки получим:
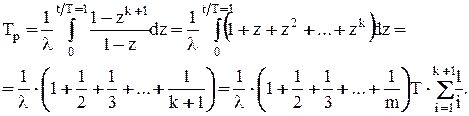
Из данного выражения следует, что выигрыш в средней наработке до отказа, полученный путем введения резервных элементов, снижается по мере увеличения кратности резервирования. Работа группы резервированных элементов характеризуется последовательным переходом от «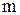 » к
» к 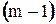 ,
, 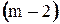 элементов и далее до одного элемента; отказ последнего элемента приводит к отказу всей группы.
элементов и далее до одного элемента; отказ последнего элемента приводит к отказу всей группы.
Работа этой группы резервированных элементов представлена на графике:
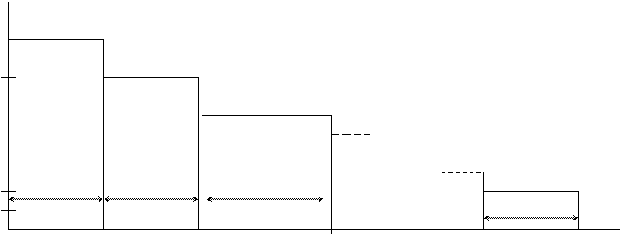 n(t)
n(t)
m
m
m-1
(m-1) (m-2)
2 λ1 =mλ λ2 =(m-1)λ λ3 =(m-2)λ 2
1 T1 T2 T3 Tm
λm =λ
t1 t2 t3 tm-1 tm
В случайные моменты времени t1,t2…tm происходят отказы элементов n(t) и число работающих элементов постепенно снижается. Поскольку на каждом участке Т1,Т2…Тm совместно функционируют m, m1 m2 … элементов, то случайные интервалы времени Т1 имеют экспоненциальноераспределение с интенсивностями отказов соответственно mλ; (m-1)λ; …λ и средней продолжительностью:
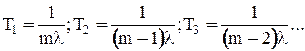 и т.д.
и т.д. 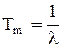
Поскольку средняя наработка до отказа группы резервированных элементов Тр = Т1+Т2+Т3+…Тm, то справедливо выражение
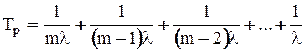 .
.
 2014-02-12
2014-02-12 1853
1853
