Декартово (прямое) произведение множеств

Декартовым произведением двух множеств А и В называют множество всех упорядоченных пар элементов из А и В. Таким образом, А ´ В ={(a, b): а Î A и b Î В }.

Обобщение на систему множеств: пусть { A ₁, A ₂, A ₃,…, A_n } конечная система множеств, тогда A ₁ ´ A ₂ ´ A ₃ ´ …´ A_n ={(a ₁, a ₂,…, a_n): a_i Î A_i, i =1,2,…, n }. Элементы (a ₁, a ₂,…, a_n) называются упорядоченными «энками» или кортежами длины n. Если множества A ₁, A ₂, A ₃,…, A_n совпадают и равны A, тогда A ₁ ´ A ₂ ´ A ₃ ´ …´ A_n обозначается Aⁿ, если A =ℝ Þ ℝ´ℝ´…´ℝ⇋ℝ ⁿ – называется n‑мерным Евклидовым вещественным пространством, а элементы этого пространства (a ₁, a ₂,…, a_n) называются n‑мерными векторами или точками.

Примеры:

1) A ={ a, b, c }; B ={0, 1} => A ´ B ={(a,0), (a,1), (b,0), (b,1), (c,0), (c,1)}.

2) A =[-2; 2]; B =[1; 3] => A ´ B ={(x, y): -2 £ x £ 2, 1£ y £ 3} – прямоугольник на вещественной плоскости.

3) A – круг радиуса r, B =[ a, b ] – отрезок. Тогда A ´ B – цилиндр радиуса r и высотой (b ‑ a).

4) A и B – окружности с несовпадающими центрами, тогда A ´ B – поверхность тора.

Множества A и B в прямом произведении А ´ В называют координатными осями, а элементы x Î А и y Î В – проекциями вектора z =(x, y)Î А ´ В на координатные оси или координатами точки z (абсциссой и ординатой соответственно). Будем обозначать их пр _А z и пр _В z.

Пусть множество М Ì А ´ В, проекцией множества М на ось А называется множество всех абсцисс векторов из М, проекцией множества М на ось В называется множество всех ординат векторов из М, т.о. пр _А М ={ пр _А z: z Î М }={ x Î А: $ y Î В и (x, y)Î М } и пр _В М ={ пр _В z: z Î М }={ y Î В: $ x Î А и (x, y)Î М }.

Для многомерного случая A ₁ ´ A ₂ ´ A ₃ ´ …´ A_n, каждое множество A_i называется i- той координатной осью. Проекция вектора z =(a ₁, a ₂,…, a_n) на i -тую координатную ось равна его i- той координате: пр _i z = a_i, где i =1,2,…, n. Если М Ì A ₁ ´ A ₂ ´…´ A_n, то пр _i М ={ пр _i z: z Î М }. Определены также проекции вектора z и множества векторов М на несколько координатных осей с номерами i ₁, i ₂,…, i_k: пр _{i 1, i 2… ik} z = (a_{i 1}, a_{i 2},…, a_ik) – k ‑мерный вектор и пр _{i 1, i 2… i k} М = { пр _{i 1, i 2… i k} z: z Î М } – множество k ‑мерных векторов.

Пример:

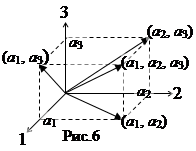Тройки вещественных чисел (а ₁, а ₂, а ₃) можно рассматривать как точку в трехмерном пространстве (или вектор, проведенный в эту точку из начала координат). Тогда пр _i (а ₁, а ₂, а ₃)= a_i, где i =1,2,3, пр _i,j (а ₁, а ₂, а ₃)=(a_i, a_j), где i,j =1,2,3. См. рис.6.