Отображения и функции

Композиция двух соответствий

Пусть Г=(G, А, В) и S=(R, B, C) – соответствия.

Композицией графиков R и G называется график R ∘ G ={(x, z): $ y Î B и (x, y)Î G и (y, z)Î R }. При этом область значений графика G является областью определения графика R, т.е. пр₂ G = пр₁ R. Композицией соответствий S и Г называется соответствие S∘Г=(R ∘ G, А, С).

При этом область прибытия Г является областью отправления S. Иными словами, под композицией понимают последовательное применение двух соответствий: сначала соответствия Г к элементам множества А, а затем соответствия S к значениям Г.

Свойства композиции.

Следующие свойства справедливы как для композиции графиков, так и для композиции соответствий с этими графиками. Пусть Г=(G, А, В), S=(R, B, C) и Р=(Т, D, A) – соответствия.

1) (R ∘ G)^-1= G ^‑1∘ R ^‑1

Доказательство: рассмотрим произвольную пару (z, x)Î(R ∘ G)^-1. Тогда по определению обратного графика (x, z)Î R ∘ G, и по определению композиции $ y Î B и (x, y)Î G и (y, z)Î R. Отсюда по определению обратного графика $ y Î B и (y, x)Î G ^‑1 и (z, y)Î R ^‑1 или, что то же самое: $ y Î B и (z, y)Î R ^‑1 и (y, x)Î G ^‑1. Отсюда по определению композиции следует (z, x)Î G ^‑1∘ R ^‑1. Аналогично можно показать, что любая пара (z, x) из G ^‑1∘ R ^‑1 принадлежит также и (R ∘ G)^-1. Отсюда следует: (R ∘ G)^-1= G ^‑1∘ R ^‑1.

2) (R ∘ G) ∘ T = R ∘ (G ∘ T)

Доказательство: рассмотрим произвольную пару (x, z)Î(R ∘ G) ∘ T. Тогда по определению композиции $ y Î A и (x, y)Î T и (y, z)Î(R ∘ G), отсюда $ y Î A и (x, y)Î T и $ t Î B и (y, t)Î G и (t, z)Î R. Последнее равносильно тому, что $ t Î B и ($ y Î A и (x, y)Î T и (y, t)Î G) и (t, z)Î R, поэтому $ t Î B и (x, t)Î(G ∘ T) и (t, z)Î R, следовательно, (x, z)Î R ∘(G ∘ T). Аналогично можно показать, что для любой пары (x, z)Î R ∘(G ∘ T) выполняется также: (x, z)Î(R ∘ G) ∘ T.

3) (R ∘ G)(A) = R (G (A))

Доказательство: рассмотрим произвольный элемент z Î(R ∘ G)(A), т.е. z является образом некоторого элемента х Î A или, что то же самое, $ x Î A и z =(R ∘ G)(x) или (x, z)Î(R ∘ G). Поэтому $ x Î A и $ y Î B и (x, y)Î G и (y, z)Î R (по определению композиции). Таким образом, z = R (y) и y = G (x) и, следовательно, $ x Î A и z = R (G (x)) или z Î R (G (A)). Далее для завершения доказательства все рассуждения проводим в обратном порядке.

График вида D _А ={(x, x): x Î A } называется диагональю А ´ А.

Очевидно, пр₁D _А =пр₂D _А = А. Соответствие I _А =(D _А, А, А) называется тождественным соответствием для А. Очевидно, I _А ^-1=I _А, и Г∘I _А = I _В ∘Г = Г, где I _В =(D _В, В, В) и Г=(G, A, B).

Пример:

Даны множества А ={ Иван, Жанн, Билл }, В ={ рус, англ, фр } и C ={ 0, 1, 2 }. И графики G ={(Иван, рус); (Иван, англ); (Жанн, фр); (Жанн, англ); (Билл, англ)} и R ={(рус, 0); (англ, 1); (фр, 2)} соответствий Г=(G, А, В) и S=(R, B, C). Тогда композицией соответствий S и Г будет соответствие S∘Г=(R ∘ G, А, С) между множествами А и С с графиком R ∘ G ={(Иван, 0); (Иван, 2); (Жанн, 1); (Жанн, 2); (Билл, 2)}

Соответствие f =(G, А, В) называется однозначным, если для всякого элемента x Îпр₁ G существует не более одного (а может быть и вовсе ни одного) значения y Îпр₂ G. Всюду определенное и однозначное соответствие называется функцией или отображением множества А в множество В. Если А и В числовые множества, то функция называется числовой.

Для отображений чаще используются обозначения вида: f: A ® B или A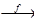B. Пару (х, у) Î G чаще обозначают y = f (x), и поскольку отображение – это частный случай соответствия, то определены все ранее введенные понятия: образа и прообраза для элементов и множеств, области определения и области значений отображения (или функции), а также понятия композиции отображений, обратного отображения, тождественного отображения, симметричного отображения.

Отображение (функция) называется постоянным, если " х ₁ ¹ х ₂Î A следует f (x ₁) = f (x ₂). Элемент х Î A называется неподвижной точкой отображения, если f (x) = x.

Отображение f: A ® B называется инъективным или взаимно-однозначным отображением множества А в В, если для " х ₁ ¹ х ₂Î A Þ f (x ₁) ¹ f (x ₂). Т.е. каждый образ имеет только один прообраз. Подчеркнем, что не все элементы множества В обязаны иметь прообраз (должны быть чьими-нибудь образами).

Отображение называется сюрьективным (или сюрьекцией или отображением множества А на множество В), если f (A) = B или " y Î B $ x Î A (один или несколько) и y = f (x), т.е. все элементы множества В являются чьими-нибудь образами (имеют по крайней мере один прообраз).

Отображение называется биективным (биекцией или взаимно однозначным отображением A на B), если оно одновременно инъективно и сурьективно.

Пример:

Сos: [0; p] ® ℝ – инъективное отображение.

Сos: ℝ ® [-1; 1] – сюрьективное, но не инъективное отображение.

Сos: [- p; 0] ® [-1; 1] – биективное отображение.

Сos: ℝ ® ℝ – не сюрьективное и не инъективное отображение.

Биекция множества A на А называется подстановкой множества A. Тождественное отображение I _A (x)= x, где x Î A, является частным случаем подстановки.

Утверждение: 1) Если f: A ® В и g: В ® С – две функции, то g ∘ f: A → C – тоже является функцией.

Действительно, т.к. композиция – это последовательное применение отображений, то для произвольного элемента x Î A с помощью функции f можно получить не более одного элемента y = f (x) Î B. В свою очередь, для элемента y Î B с помощью функции g можно получить не более одного элемента z = g (y)Î C. Тем самым, для каждого x Î A с помощью (g ∘ f) можно получить не более одного элемента z Î C, следовательно, (g ∘ f) – функция и (g ∘ f)(x)= g (f (x)).

2) Пусть f: A ® В – функция. Для того, чтобы f ^‑1: В ® А было функцией, необходимо и достаточно, чтобы f было биективным отображением. В этом случае f ^–1 называется отображением, обратным к f, или обратной функцией. При этом f ^‑1 – биективно, f ^‑1∘ f =I _A – тождественное отображение А и f ∘ f ^‑1=I _B – тождественное отображение В.

Отображение f: A ® В называется обратимым слева (справа), если существует отображение f _Л^‑1: В ® А (f _П^‑1: В ® А) такое, что f _Л^‑1∘ f =I _A (f ∘ f _П^‑1=I _B).

Критерий обратимости слева (справа)

Для того, чтобы отображение f: A ® В было обратимым слева (справа), необходимо и достаточно чтобы оно было инъективным (сюрьективным).

Примеры отображений:

1) Пусть f (x) = x ²+1 и g (x) = 2– x – две числовые функции, определенные на множестве ℝ. Тогда область значений f (x) – это множество B ={ x Îℝ: x ³1}, а g (x) – множество ℝ. Отображение f:ℝ® B – сюрьекция, а g:ℝ®ℝ – биекция. Композиция (g ∘ f)(х)= g (f (х)) = 2–(x ²+1) = 1– x ²; (f ∘ g)(х) = f (g (х)) =(2– x)²+1 = 5–4 x + x ². Обратное отображение g ^–1(х)= 2– x, т.е. g (x) – симметричная функция. И (g ∘ g ^-1)(х) = (g ^-1∘ g)(x) = х. Отображение f (x) не имеет обратной функции, но обратимо справа, как сюрьекция. При этом f _П1^‑1(х)=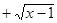или f _П2^‑1(х)=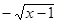, где x Î B и имеются в виду только положительные значения корня. Для каждого из f _{П k} ^‑1(х) (k =1,2) композиция (f ∘ f _{П k} ^‑1)(х)=I _B (x)= x.

Образ х =2 для f (x) = f (2) =5; для g (x) = g (2) = 0.

Если множество А =[-1; 2], то образ f (A) = [1; 5] и g (A) = [0; 3]

Уравнение f (x) = x не имеет корней, поэтому f (x) не имеет неподвижных точек. Неподвижной точкой g (x) является x = 1.

2) Пусть f и g: ℝ²® ℝ² осуществляет параллельные переносы всех точек плоскости, причем f переносит каждую точку на 2 единицы вправо (на восток), а g на 2 единицы вверх (на север). Тогда f ^–1 переносит каждую точку плоскости на 2 единицы влево (на запад), а g ^‑1– на 2 единицы вниз (на юг). Композиция f ∘ g – осуществляет параллельный перенос каждой точки к северо-востоку на 2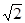ед., аналогично g ∘ f то же самое. А (f ∘ g)^-1 и (g ∘ f)^-1 переносят точки к юго-западу на 2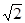ед.. Композиции f ∘ f ^–1 и g ∘ g ^-1 оставляют каждую точку плоскости на месте. Оба отображения биективны.

3) «Подобие плоскости» – это функция f: ℝ²® ℝ², изменяющая все длины в одно и то же число раз = r >0, где длины измеряются относительно некоторой фиксированной точки плоскости z Îℝ², обычно это точка с координатами (0,0). Тогда при r >1 функция f задает растяжение, а при r <1 – сжатие с центром z. Эта функция взаимно-однозначна. Отображение f ^–1, обратное к растяжению с коэффициентом r >1, есть сжатие с коэффициентом 1/ r и тем же центром.

4) Пусть A ={1, 2, 3, 4} и f и g – две подстановки множества A. Запишем каждую подстановку в виде двух строк, где в первой строке перечислим элементы множества A, а во второй – соответствующие им элементы f (a_i) и g (a_i): 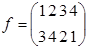и 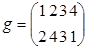– такая запись подстановок является традиционной.

Тогда 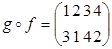, , 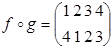, 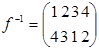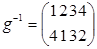и 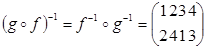, , 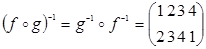и, наконец, 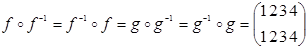– тождественная подстановка множества A.

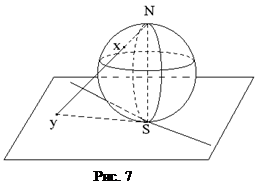5) «Стереографическая проекция». Рассмотрим отображение f: A ®ℝ², где АÍℝ³ – сфера без северного полюса N, ℝ² – плоскость, параллельная экватору и касающаяся сферы в точке S. Каждой точке х сферы (за исключением N) функция f ставит в соответствие точку плоскости у, в которой луч N x пересекает плоскость. См. рис.7. Тогда:

а) образом произвольной параллели сферы будет окружность с центром в точке S, образ экватора – окружность вдвое большего радиуса, чем сфера;

б) образом произвольного меридиана будет прямая, проходящая через S;

в) прообраз произвольного луча из S есть полуокружность, проходящая через S и N, за исключением точки N;

г) прообразом произвольного прямолинейного отрезка на плоскости является дуга некоторой окружности, по которой плоскость, проходящая через N и отрезок, пересекает сферу.