511
Пусть производится n независимых опытов, в каждом из которых с одинаковой вероятностью р может произойти некоторое событие А. Случайная величина Х – число опытов, в которых произошло событие А– распределена по биномиальному закону распределения
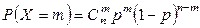(7.1)
с рядом распределения
| xi | . . . | m | . . . | n | ||
| pi | (1-p)n | np(1-p)n-1 | . . . | Cnm pm(1-p)n-m | . . . | pn |
Где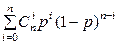 
= 1.
Для доказательства данного факта следует сумму 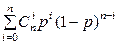рассматривать как разложения бинома Ньютона с переменными р и (1-р), т.е.
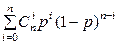= [ p + (1 – p) ]n = 1 .
Биномиальный закон распределения имеет два параметра:
р – вероятность появления событие Ав одном опыте;
n– общее число опытов (испытаний).
Вероятность попадания дискретной случайной величины, распределенной по биномиальному закону, в заданный диапазон значений определяется с помощью формулы
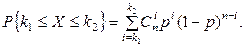(7.2)
