473
Второй центральный момент μ2 называется дисперсией D(X)и характеризует степень разбросаслучайной величины вокруг ее математического ожидания.
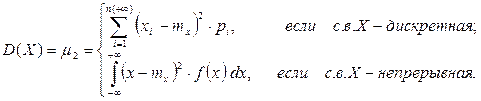(6.10)
Дисперсия имеет размерность квадрата случайной величины.
На рис.6.5 показаны две непрерывные случайные величины, заданные в виде плотности распределения c одинаковыми математическими ожиданиями (mх2 = mх1) и отличающиеся друг от друга своей дисперсией (Dх2 > Dх1).
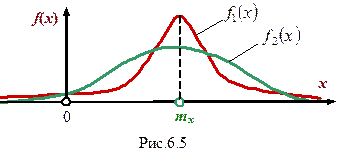
Определение дисперсии Dx для непрерывных случайных величин связано с трудоемкими вычислениями определенных интегралов. На практике дисперсию вычисляют с помощью второго начального момента α2 и математического ожидания (первого начального момента) mх.
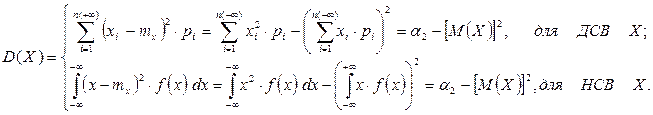
Таким образом
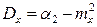. (6.11)
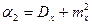(6.12)
