Средняя арифметическая взвешенная
Средняя арифметическая простая
Задача 2. Определите среднюю выработку пяти рабочих цеха за рабочую смену по следующим данным: 10 шт., 20 шт., 17 шт.,15 шт., 12 шт.
Задача 3. Определите среднюю выработку одного рабочего за рабочую смену по следующим данным (продукция однотипная):
| Выработка, шт. | Число рабочих, чел. |
| Итого: |
Решение:
Вывод: Если известны значения знаменателя, но не известны значения числителя в ИСС, то средняя вычисляется по формуле средней арифметической взвешенной.
1) Сумма отклонений значений признака X от средней арифметической равна нулю:
Доказательство:
2) Если веса (частоты) каждого значения признака X умножить или разделить на постоянное число, то средняя не изменится.
Доказательство:
3) Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то средняя увеличится или уменьшится во
столько же раз.
Доказательство:
Следствие: Общий множитель индивидуальных значений признака X может быть вынесен за знак средней:
4) Средние суммы (разности) двух или нескольких величин равна сумме (разности) их средних: 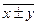 =
= 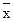 ±
± 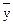
Доказательство:
5) Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа.
Доказательство:
6) Если к каждому индивидуальному значению признака X прибавить или вычесть постоянное число, то и средняя величина возрастет или уменьшится на то же число.
Доказательство:
 2014-02-12
2014-02-12 413
413








