2014-02-12
511
Таблица 7.2.
Таблица 7.1.
Задача №1.
При выборочном обследовании 10% изделий партии готовой продукции по методу бесповторного отбора получены следующие данные о содержании влаги в образцах:
| Влажность, % | Середина интервала | Число образцов |
| До 13 | ||
| 13-15 | ||
| 15-17 | ||
| 17-19 | ||
| 19 и выше | ||
| Итого |
На основании данных выборочного обследования:
1) Определите ошибку выборочной средней;
2) Определите ошибку выборочной доли, если известно, что к стандартной продукции относятся изделия с влажностью 13-19%;
3) Определите возможные пределы с вероятностью 0,954,в которых ожидается средний процент влажности всей готовой продукции;
4) С вероятностью 0,997 возможные пределы удельного веса стандартной продукции.
Решение:
Формулы средней ошибки (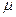
) выборочной средней и выборочной относительной величины (доли)
| Вид выборки | Средняя ошибка | |
| Выборочной средней | Выборочной доли | |
| 1. Повторная – отбор единицами |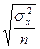 
| 
|
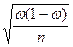
| 2. Бесповторная - отбор единицами |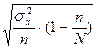 
| 
|
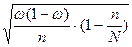
| 3. Серийная |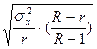 
| 
|
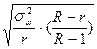
| 4. Типическая (районированная)- отбор единицами. |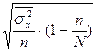 
| 
|
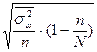
| 5.Типическая отбор сериями |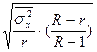 
| 
|
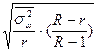
3. дисперсия (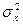
) определяется как колеблемость между сериями:
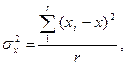
где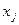 
- среднее значение признака x в j серии;
r- число обратных серий
R- число серий в генеральной совокупности;
,
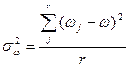где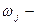 
доля единиц определенной категории в 
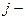серии;
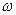- доля единиц этой категории в выборочной совокупности.
4. 
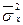- это средняя из внутрирайонных дисперсий.
,
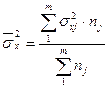где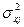 
– выборочная дисперсия признака 
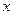в 
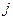–м районе;
,
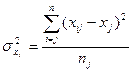где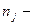 
объем выборки в j-м районе;
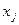- средняя в j-м районе;
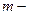число районов.
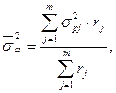
где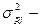 
межсерийная дисперсия доли в 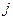–м районе;
7. 4. Малая выборка.
Под малой выборкой понимается
При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента:
где 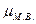 . – мера случайных колебаний выборочной средней в малой выборке.:
Дисперсия при малой выборке:
Предельная ошибка малой выборки рассчитывается аналогичным образом:
Но, в данном случае, вероятная оценка зависит не только от величины t, но и от объема выборки. Величина коэффициента доверия t при различных объемах малой выборки представлена в таблице 7.2.
Доверительные интервалы для малой выборки:
|
