2014-02-12
959
Если поставить задачу определения верхней границы допускаемой ошибки с заданной доверительной вероятностью g, то есть поиска числа d, для которого
,
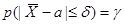то получим известную задачу определения доверительного интервала для математичес-кого ожидания генеральной совокупности (см. лекцию 18). Воспользуемся результатами решения этой задачи для следующих случаев:
1) случайная величины Х распределена нормально и известно ее среднее квадратическое отклонение. Тогда из формулы (18.1) получаем: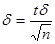 
, где п – число испытаний, s - известное среднее квадратическое отклонение, а t – аргумент функции Лапласа, при котором Ф(t) = g/2.
2) Случайная величина Х распределена нормально с неизвестным s. Воспользуемся формулой (18.3), из которой следует, что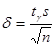 
, где s – исправленное выборочное среднее квадратическое отклонение, а 
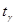определяется по соответствующей таблице.
3) Если случайная величина распределена по иному закону, то при достаточно большом количестве испытаний (n > 30) можно использовать для оценки d предыдущие формулы, так как при п ®¥ распределение Стьюдента стремится к нормальному, и границы интервалов, полученные по формулам (18.1) и (18.3), различаются незначительно.
