Определение дискретной случайной величины
ПОНЯТИЕ О ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИНАХ
В этом разделе предполагается, что в пространстве элементарных исходов конечное или счетное число исходов (бесконечное множество называется счетным, если его элементы можно пронумеровать числами натурального ряда 1, 2, 3, …, 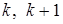 , …).
, …).
Дискретной случайной величиной называется произвольная числовая функция, определенная на пространстве W с конечным или счетным числом исходов; каждому элементарному исходу 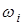 ставится в соответствие число
ставится в соответствие число 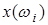 ,называемое значением случайной величины на исходе
,называемое значением случайной величины на исходе 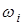 . Обозначаются случайные величины большими латинскими буквами, как правило, из конца алфавита, например, X, Y, Z.
. Обозначаются случайные величины большими латинскими буквами, как правило, из конца алфавита, например, X, Y, Z.
Соответствие 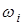 Þ x (
Þ x (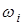 ) не обязательно взаимно однозначно. Нескольким элементарным исходам может соответствовать одно и то же число х.
) не обязательно взаимно однозначно. Нескольким элементарным исходам может соответствовать одно и то же число х.
Так как число исходов счетно или конечно, то у каждого элементарного исхода 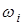 есть вероятность рi> 0 произойти (сумма всех вероятностей равна, разумеется, 1). Поэтому каждому значению хi случайной величины Х можно приписать вероятность рi, равную сумме вероятностей элементарных исходов, на которых случайная величина Х равна хi. Если конечно или счетно число исходов, конечно или счетно число разных значений xi. Совокупность всех пар {(хi, рi)} называется законом распределения случайной величины Х. Часто закон распределения задают в виде таблицы из двух строк. Она называется таблицей вероятностей. В первой строке стоят числа хi, во второй строке стоят соответствующие вероятности рi, причем
есть вероятность рi> 0 произойти (сумма всех вероятностей равна, разумеется, 1). Поэтому каждому значению хi случайной величины Х можно приписать вероятность рi, равную сумме вероятностей элементарных исходов, на которых случайная величина Х равна хi. Если конечно или счетно число исходов, конечно или счетно число разных значений xi. Совокупность всех пар {(хi, рi)} называется законом распределения случайной величины Х. Часто закон распределения задают в виде таблицы из двух строк. Она называется таблицей вероятностей. В первой строке стоят числа хi, во второй строке стоят соответствующие вероятности рi, причем 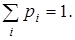 Пишут еще так:
Пишут еще так: 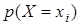 .
.
Рассмотрим несколько примеров случайных величин.
Пример1. Бросают три монеты. Случайная величина Х – число выпавших гербов. Пространство элементарных исходов состоит из 8 элементов: W= { ГГГ (3), ГРГ (2), ГГР (2), ГРР (1), РГГ (2), РГР (1), РРГ (1), РРР (0)}. В скобках после каждого элементарного исхода стоит соответствующее ему значение случайной величины. Всего случайная величина Х принимает 4 возможных значения: 0, 1, 2, 3. Полную вероятность каждого значения можно вычислить по формуле Бернулли.
Закон распределения случайной величины Х задается таблицей:
(табл. 7.1)
Таблица 7.1
| хi | ||||
| рi | 1/8 | 3/8 | 3/8 | 1/8 |
Для контроля: 1/8 + 3/8 + 3/8 + 1/8 = 1.
Пример 2. В урне лежат 2 белых и 3 черных шара. Наудачу извлекают 3 шара. Случайная величина Y – число белых шаров в выборке. Она принимает 3 значения – 0, 1, 2. Вероятности этих значений подсчитываются по классическим правилам:
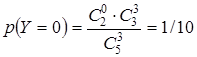 ;
; 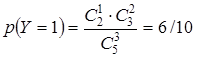 ;
; 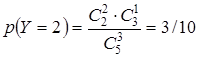 .
.
Закон распределения случайной величины Y задается так (табл. 7.2):
Таблица 7.2
| уi | |||
| рi | 0,1 | 0,6 | 0,3 |
Для контроля: 0,1 + 0,6 + 0, 3 = 1.
Пример3. Кубик бросают до первого появления единицы. Случайная величина Z – число бросаний до появления первой единицы. Возможные значения случайной величины Z – числа 0, 1, 2, 3, … Вероятности этих значений вычисляются из условия независимости бросаний (если Z =k, это означает, что в первых k бросаниях единица не появлялась, а на (k + 1) - м бросании выпала).
Закон распределения случайной величины Z имеет вид (табл. 7.3):
Таблица 7.3
| zi | ... | k | … | |||
| рi | 1/6 | (5/6)·(1/6) | (5/6)2·(1/6) | … | (5/6) k ·(1/6) | … |
Для контроля: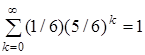 .
.
Определим функции дискретной случайной величины. Пусть Х - дискретная случайная величина с законом распределения {(хi, рi)}; φ (x) –некоторая числовая функция, определенная для всех значений хi. Дискретная случайная величина Y с законом распределения { φ (хi), рi } называется функцией случайной величины Х и обозначается Y = φ (Х).
Пусть, например, случайная величина Х задана таблицей вероятностей (табл. 7.4):
| Таблица 7.4 | |||||
| xi | -2 | -1 | |||
| pi | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Составим таблицы вероятностей случайных величин 2 Х – 1, Х 2 + 1,2 Х (табл. 7.5 - 7.7)
Таблица 7.5
| 2 хi - 1 | -5 | -3 | -1 | ||
| рi | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Таблица 7.6
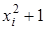
| |||
| рi | 0,3 | 0,5 | 0,2 |
Таблица 7.7
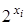
| 0,25 | 0,5 | |||
| рi | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Поясним, как составлен закон распределения случайной величины Х 2 + + 1. Эта случайная величина принимает три возможных значения: 1, если Х= 0; 2, если Х= 1 или Х= -1; 5, если Х= 2 или Х= -2. Поэтому
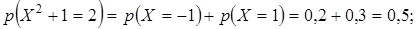
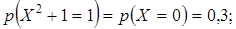
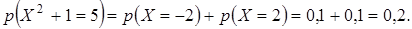
 2014-02-12
2014-02-12 471
471








