2378
Рис.7.1
Задача 60. Найти функцию распределения дискретной случайной величины Х, заданной законом распределения (табл. 7.8), и построить ее график.
Таблица 7.8
| xi | -3 | |||
| pi | 0,4 | 0,1 | 0,2 | 0,3 |
В соответствии с определением F(x) разобьем всю числовую ось на следующие интервалы:
1. 
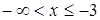; для всех x из этого интервала F(x) = 0.
2. 
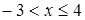; для всех x из этого интервала F(x) = 0,4.
3. 
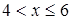; для всех x из этого интервала F(x) = 0,5.
4. 
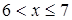; для всех x из этого интервала F(x) = 0,7.
5. 
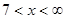; для всех x из этого интервала F(x) = 1.
Таким образом,
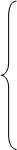0 при ;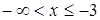
0,4 при ;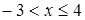
F(x) = 0,5 при ;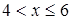
0,7 при ;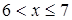
1,0 при .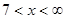
График построенной функции показан на рис. 7.2.
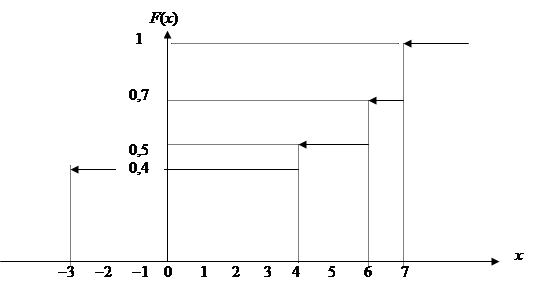
Рис.7.2
Задача 61. Урна содержит один красный и два белых шара, одинаковых во всем, кроме цвета. Из урны выбирают три шара так, что перед выбором следующего шара предыдущий шар возвращается в урну (выборка с возвращением). Найти биноминальное распределение числа красных шаров в выборке.
Решение. В данном случае производится n = 3 независимых испытаний. Каждое из испытаний состоит в выборе одного шара из трех. “Успех” – извлечение красного шара. Вероятность “успеха” р = 1/3. “Неудача” – извлечение белого шара. Вероятность “неудачи” q = 2/3. Биноминально распределенная случайная величина Х – число появлений “успеха” – может принимать четыре значения: от 0 до 3. Вычислим их вероятности по формуле Бернулли:
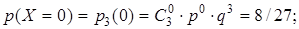
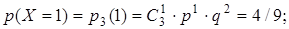
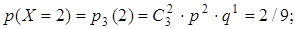
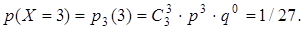
Составим таблицу вероятностей случайной величины Х (табл. 7.9).
Таблица 7.9.
| ||||
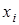| pi | 8/27 | 4/9 | 2/9 | 1/27 |
Для контроля: 8/27 + 4/9 + 2/9 + 1/27 = 1.
Задача 63. Дана таблица вероятностей случайной величины Х (табл.7.11).
Таблица 7.11
| xi | |||||||
| pi | С | 2С | 2С | 4С | С2 | 2С2 | 7С2 |
1. Найти С. 2. Вычислить р(Х ³5)и р(Х <3).
Решение.
1. Константа С находится из условия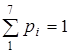 
. Имеем 9С + 10С2 = 1, откуда С1 = -1; С2 = 0,1.
Вероятности не могут быть отрицательными, поэтому остается одно значение: С = 0,1. Таблица вероятностей случайной величины Х такова: (табл. 7.12)
Таблица 7.12
| xi | |||||||
| pi | 0,1 | 0,2 | 0,2 | 0,4 | 0,01 | 0,02 | 0,07 |
2. Событие {Х ³5} есть в данном случае сумма следующих несовместных событий: А = {Х = 5}, В = {Х = 6}, С = {Х = 7}, р(Х ³5) = р(А) + р(В) +
+ р(С) = 0,1. Аналогично р(Х < 3) = р(Х = 2) + р(Х = 1) = 0,3.
