Некоторые распределения (биноминальное, Пуассона,
Биноминальное распределение. Случайная величина Х называется распределенной по биноминальному закону, если ее возможные значения - числа 0, 1, 2, …, n, а соответствующие вероятности вычисляются по формуле Бернулли:
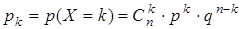 где
где 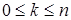 , q= 1 – p, 0 < p< 1.
, q= 1 – p, 0 < p< 1.
Это распределение зависит от двух параметров: p и n. Например, случайная величина Х – число появлений “успеха” в n независимых испытаниях – имеет биноминальное распределение.
Распределение Пуассона. Дискретная случайная величина Х называется распределенной по закону Пуассона, если ее возможные значения - числа 0, 1, 2, …, k, …, а соответствующие вероятности вычисляются по формуле Пуассона:
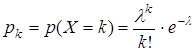 , где k = 0, 1, 2,…, λ > 0.
, где k = 0, 1, 2,…, λ > 0.
Распределение зависит от параметра λ. Распределение Пуассона является предельным для биноминального, если устремить значение параметра n кбесконечности и положить λ = np = const. Пользоваться формулой Пуассона вместо формулы Бернулли разумно, когда n велико, а вероятность p мала.
Геометрическое распределение. Дискретная случайная величина Х имеет геометрическое распределение, если ее возможные значения - числа 0, 1, 2, …, k,… Соответствующие вероятности вычисляют по формуле
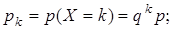 p+ q= 1, где 0 < p < 1, k = 0, 1, 2,….
p+ q= 1, где 0 < p < 1, k = 0, 1, 2,….
Вероятности рк образуют бесконечно убывающую геометрическую прогрессию со знаменателем q. Геометрическое распределение получается, если производится ряд независимых попыток получить некоторый “успех”. Вероятность “успеха” в каждом испытании равна р. Случайная величина Х – число испытаний до первого “успеха”. Геометрическое распределение зависит от одного параметра р. Иногда рассматривают случайную величину Y, равную числу испытаний до первого “успеха”, включая удавшееся. Вероятности значений величины Y:
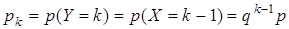 , где k = 1, 2,….
, где k = 1, 2,….
Такое распределение называют начинающимся с 1.
Гипергеометрическое распределение. Случайная величина Х имеет гипергеометрическое распределение с параметрами n, a, b, если она может принимать значения 0, 1, 2, … a с вероятностями
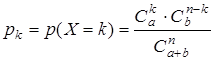 , где k = 0, 1, 2, …, a; a + b ³ n ³ k; a, b, n - натуральные числа.
, где k = 0, 1, 2, …, a; a + b ³ n ³ k; a, b, n - натуральные числа.
Гипергеометрическое распределение возникает, например, в такой ситуации. Имеется урна, в которой a белых и b черных шаров. Из нее вынимают наудачу n шаров. Случайная величина Х – число вынутых белых шаров - имеет гипергеометрическое распределение.
Докажем, что сумма вероятностей значений случайных величин, имеющих биноминальное, пуассоновское, геометрическое и гипергеометрическое распределения, равна 1.
1. Равенство единице суммы биноминальных вероятностей было доказано в разделе 6.
2. 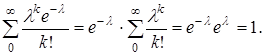
3. 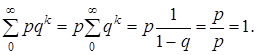
 4. Суммировать вероятности гипергеометрического закона нет необходимости, т. к. события Нk = { Х = k }, k = 0, 1, 2, …, a образуют разбиение классического пространства элементарных исходов, в котором всего
4. Суммировать вероятности гипергеометрического закона нет необходимости, т. к. события Нk = { Х = k }, k = 0, 1, 2, …, a образуют разбиение классического пространства элементарных исходов, в котором всего 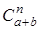 исходов. Поэтому сумма этих вероятностей равна 1.
исходов. Поэтому сумма этих вероятностей равна 1.
 2014-02-12
2014-02-12 3823
3823








