2014-02-12
339
ВЕЛИЧИН, ОПРЕДЕЛЕННЫХ НА ОДНОМ И ТОМ ЖЕ
РАСПРЕДЕЛЕНИЕ ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ
Пусть на одном и том же пространстве элементарных исходов Ω заданы две дискретные случайные величины Х и Y с законами распределе-
ния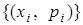 
и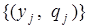 
соответственно. Тогда события Аi = { Х = xi }, где i = 1, 2, … и события Вj = { Y = уj }, где j = 1, 2, … образуют разбиение множества Ω.
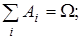
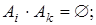(i ¹ k),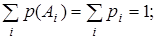 
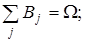
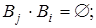(j ¹ i),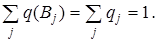 
Следовательно, образуют разбиение множества W и попарные произведения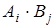 
: 
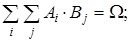
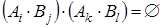, i ¹ k или j ¹ ¹ l.
Обозначим вероятности произведений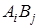 
символами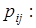 
= 
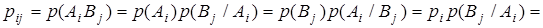
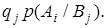(8.1)
Вероятности рij задают совместное распределение случайных величин Х и Y. Говорят еще, что задана система случайных величин Х, Y или случайный вектор (Х, Y).
Случайные величины Х, Y называются независимыми тогда и только тогда, когда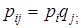 
i = 1, 2, …; j = 1, 2, …. (8.2)
Если случайные величины Х, Y принимают конечное число значений: i = 1, 2, …m; j = 1, 2, …n, то вероятности рij можно записать в таблице с m строками и n столбцами (табл. 8.1). Заметим, что
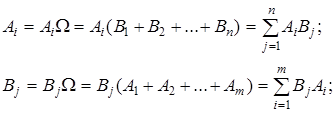
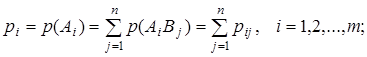
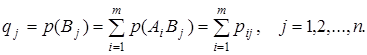
Таблица 8.1
 yj
xi
| y 1 | … | yj | … | yn | pi |
| x 1 | p 11 | … | p 1 j | … | p 1 n |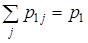 
|
| … | … | … | … | … | … | … |
| xi | pi 1 | … | pij | … | Pin |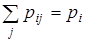 
|
| … | … | … | … | … | … | … |
| xm | pmi | … | pmj | … | Pmn |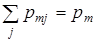 
|
| qj |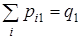 
| … | 
| … | 
| 
|
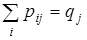
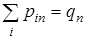
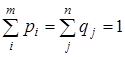
Кроме того,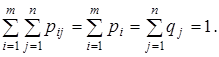 
|
|
|
В дальнейшем, когда речь пойдет о двух и более случайных величинах, всегда будет подразумеваться, что они определены на одном и том же пространстве Ω.
