8.4.1. Заданы независимые случайные величины Х и Y:
| xi | -1 | yj | |||||||
| pi | 0,2 | 0,5 | 0,3 | qj | 0,2 | 0,4 | 0,3 | 0,1 |
Составить законы распределения случайных величин Х + Y, ХY, Х 2 + Y 2.
Решение. Указанные законы распределения приведены в табл. 8.11 - 8.13.
Таблица 8.11
| xi + yj | -1 | |||||
| pij | 0,04 | 0,18 | 0,32 | 0,29 | 0,14 | 0,03 |
Таблица 8.12
| xiyj | -3 | -2 | -1 | ||||
| pij | 0,02 | 0,06 | 0,08 | 0,6 | 0,12 | 0,09 | 0,03 |
Таблица 8.13
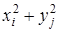 | |||||||
| pij | 0,1 | 0,3 | 0,2 | 0,15 | 0,05 | 0,15 | 0,05 |
Поясним, например, как получился закон распределения случайной величины ХY. Возможны 7 значений произведений xi yj: -1, -2, -3, 0, 1, 2, 3. Вероятности этих значений таковы:
p (XY = -3) = p (X = -1, Y = 3) = p (X = -1 )·p (Y = 3) = 0,2·0,1 = 0,02;
p (XY = -2) = p (X = -1, Y = 2) = 0,2·0,3 = 0,06;
p (XY = -1) = p (X = -1, Y = 1) = 0,2·0,4 = 0,08;
p (XY = 0) = p (X = 0 или Y = 0) = p (X = 0) + p (Y = 0) – p (X = 0)× p (Y = 0) =
= 0,5 + 0,2 – 0,5·0,2 = 0,6;
p (XY = 1) = p (X = 1)× p (Y = 1) = 0,3·0,4 = 0,12;
p (XY = 2) = p (X = 1) × p (Y = 2) = 0,3·0,3 = 0,09;
p (XY = 3) = p (X = 1) × p (Y = 3) = 0,3·0,1 = 0,03;
Контроль: 0,02 + 0,06 + 0,08 + 0,6 + 0,12 + 0,09 + 0,03 = 1.
Поясним еще, как была вычислена вероятность события { Х 2 + Y 2 = 5}.
p (Х 2 + Y 2 = 5)= p (X = -1, Y = 2 или X = 1, Y = 2) = p (X = -1) × p (Y = 2) +
+ p (X = 1) ×p (Y = 2) = 0,2·0,3 + 0,3·0,3 = 0,15.
8.4.2. Ниже для каждой пары значений (xi, yj) дискретных случайных величин Х и Y заданы вероятности pij (табл. 8.14). Найти закон распределения суммы Z = Х + Y.
Таблица 8.14
| yj xi | ||||
| -1 | 0,01 | 0,06 | 0,05 | 0,04 |
| 0,04 | 0,24 | 0,15 | 0,07 | |
| 0,05 | 0,10 | 0,10 | 0,09 |
Решение. Сумма Х + Y принимает следующие значения: -1, 0, 1, 2, 3, 4. Найдем соответствующие вероятности.
p (X + Y = -1) = p (X = -1, Y = 0) = 0,01;
p (X + Y = 0) = p (X = -1, Y = 1) + p (X = 0, Y = 0) = 0,06 + 0,04 = 0,1;
p (X + Y = 1) = p (X = -1, Y = 2) + p (X = 0, Y = 1) + p (X = 1, Y = 0) =
= 0,05 + 0,24 + 0,05 = 0,34;
p (X + Y = 2) = p (X = -1, Y = 3) + p(X = 0, Y = 2) + p (X = 1, Y = 1) =
= 0,04 + 0,15 + 0,1 = 0,29;
p (X + Y = 3) = p (X = 0, Y = 3) + p (X = 1, Y = 2) = 0,07 + 0,1 = 0,17;
p (X + Y = 4) = p (X = 1, Y = 3) = 0,09.
Этот закон распределения (вероятности обозначены 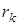 ) задан в табл. 8.15.
) задан в табл. 8.15.
Таблица 8.15
| zк | -1 | |||||
| rк | 0,01 | 0,1 | 0,34 | 0,29 | 0,17 | 0,09 |
Контроль: 0,01+ 0,1 + 0,34 + 0,29 + 0,17 + 0,09 = 1.
8.4.3. Две независимые случайные величины Х и Y имеют такие законы распределения (табл. 8.16 и 8.17).
Таблица 8.16 Таблица 8.17
| xi | yj | -1 | |||||||
| pi | 0,3 | 0,2 | 0,1 | 0,4 | qj | 0,2 | 0,1 | 0,7 |
Построить закон распределения случайной величины Z = min(X, Y).
Решение. Для удобства составления закона распределения случайной величины Z представим ее возможные значения - числа zij и вероятности этих значений - произведения 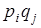 в таблицах (табл. 8.18 и 8.19).
в таблицах (табл. 8.18 и 8.19).
Таблица 8.18 Таблица 8.19
  yj xi yj xi | -1 | qj pi | 0,2 | 0,1 | 0,7 | |||
| -1 | 0,3 | 0,06 | 0,03 | 0,21 | ||||
| -1 | 0,2 | 0,04 | 0,02 | 0,14 | ||||
| -1 | 0,1 | 0,02 | 0,01 | 0,07 | ||||
| -1 | 0,4 | 0,08 | 0,04 | 0,28 |
Закон распределения случайной величины Z представлен в табл. 8.20.
Таблица 8.20
| zi | -1 | ||||
| pi | 0,2 | 0,24 | 0,16 | 0,08 | 0,32 |
Контроль: 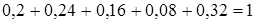 .
.
 2014-02-12
2014-02-12 6440
6440