Примеры решения задач. 8.1.1. Некоторый вид биологической клетки подвергается воздействию, при котором клетка погибает с вероятностью 0,25 и делится на две клетки с вероятностью

8.1.1. Некоторый вид биологической клетки подвергается воздействию, при котором клетка погибает с вероятностью 0,25 и делится на две клетки с вероятностью 0,75. Пусть Х – число живых клеток после воздействия на одну клетку, Y – число живых клеток после воздействия на Х клеток. Клетки реагируют на воздействие независимо друг от друга, и умершая клетка не оживает. Найти:

а) закон распределения системы (Х, Y);

б) законы распределения Х и Y в отдельности;

в) закон распределения Y при условии, что Х = 2. Зависимы ли случайные величины Х и Y?

Решение. Пространство W состоит из пяти исходов:

(0,0) (2,0) (2,2) (2,2) (2,4)

W = { (0) (20) (22₁) (22₂) (24)}.

Здесь запись 20, например, означает, что первая клетка поделилась на две, но при последующем воздействии обе они погибли. Запись 22₂ означает, что первая клетка поделилась на две, а затем первая из этих двух клеток погибла, а вторая поделилась на две. Запись 0 означает, что исходная клетка погибла.

Сверху в скобках над элементарными исходами записаны значения случайных величин Х, Y, соответствующие этим исходам.

Случайная величина Х принимает два значения: 0 и 2; случайная величина Y принимает три значения: 0, 2, 4. Соответствующие вероятности обозначим через р ₁, р ₂и q ₁, q ₂, q ₃. Из условия задачи следует:

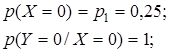
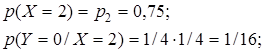
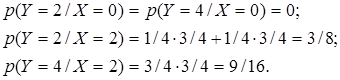
Отсюда:

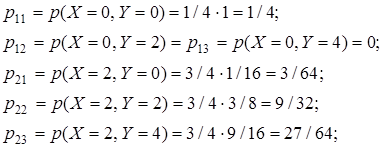
Тогда:

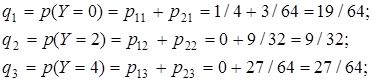
Совместное распределение Х и Y задано в табл. 8.2.

Таблица 8.2

yj xi				pi
	1/4			1/4
	3/64	9/32	27/64	3/4
qj	19/64	9/32	27/64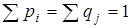

Законы распределения величин Х и Y в отдельности, а также закон распределения величины Y при условии, что Х = 2, заданы в табл. 8.3 - 8.5.

Таблица 8.3 Таблица 8.4

xi				yj
pi	1/4	3/4	qj	19/64	9/32	27/64

Таблица 8.5

yj
p (yj/X= 2)	1/16	3/8	9/16

Случайные величины Х и Y зависимы.

8.1.2. Закон распределения системы (Х, Y) задан таблицей:

yj xi	-1
-1	0,1	0,2		0,1
	0,05	0,1	0,05
	0,1	0,05	0,15	0,1

Найти:

а) законы распределения случайных величин Х и Y в отдельности;

б) закон распределения Х при условии, что Y = 1;

в) вероятность события { Х < 1, Y ³ 1}.

Решение.

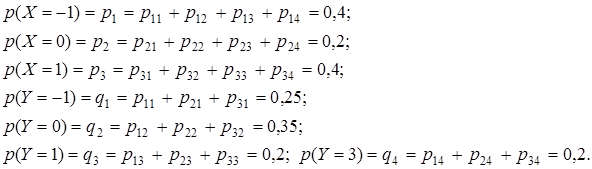
Законы распределения случайных величин Х и Y заданы в табл. 8.6 - 8.7.