Общая логика статистического вывода

Таблица 2. Данные о возрастном составе группы

Возрастная группа	Частоты	%	Накопленные частоты	Накопленные %
20-29		40,0		40,0
30-39		26,7		66,7
40-49		16,7		83,4
50-59		10,0		93,4
60-69		6,7		100,1
Всего		100,1		100,1

В первом столбце представлены возрастные интервалы. Обратим внимание, что они не пересекаются, то есть мы берем интервалы 20 — 29, 30 — 39, а не 20 — 30, 30 — 40. Иначе неясно будет, куда относить индивидов, попадающих на стык возрастных групп. Во втором и третьем столбцах представлены соответственно частоты и проценты. Глядя на них, мы видим, что возрастной состав группы неоднородный: в ней преобладают молодые люди, а люди старших возрастов встречаются реже.

В четвертом и пятом столбцах частоты и проценты представлены в несколько иной форме, которая применима для упорядоченных категорий (шкал порядка или отношений). Частоты и проценты суммируются по всем предыдущим категориям. При такой форме представления данных хорошо видно, сколько человек или какая доля выборки находятся ниже (или выше) определенного уровня. В нашем примере 25 человек из 30, или 83,4 %, моложе пятидесяти лет.

Данные о распределении переменной можно представить не только в форме таблиц, но и в форме графиков, которые еще более наглядны. Рассмотрим четыре типа графиков, которые чаще всего используются в случае одномерного распределения. Для неупорядоченных категорий (шкала наименований) обычно применяют столбиковые диаграммы. Число столбиков соответствует числу категорий. Высота каждого столбика отражает частоту встречаемости данной категории. Все столбики рисуются одинаковой ширины и не соприкасаются друг с другом. Порядок их расположе­ния на горизонтальной оси может быть любым. Для представления долей и процентов удобны круговые диаграммы. Весь круг соответствует единице или ста процентам, а величина каждого сектора отражает представительство соответствующей категории.

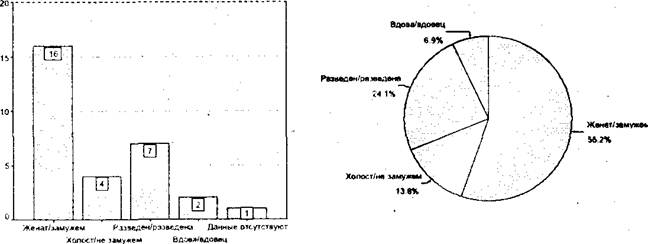
Рис. 1. Столбиковая диа- Рис. 2. Круговая диаграмма

грамма (Данные из Табл.1) (Данные из Табл. 1)

Для наглядного представления измеренных данных (шкала равных интервалов) используются так называемые гистограммы и полигоны. Гистограмма похожа на столбиковую диаграмму, только на горизонтальной оси в этом случае указываются границы интервалов. Столбики примыкают друг к другу. Высота столбика соответствует наблюдаемой частоте. Гистограмму легко преобразовать в полигон. Для этого середины вершин каждого столбца соединяются между собой прямыми отрезками. Получается ломаная линия, повторяющая контур, образуемый столбиками. Гистограмма удобна для изображения особенностей одного распределения. Преимущество полигона заключается в том, что на одном графике можно представить несколько полигонов и затем сравнивать между собой разные выборки.

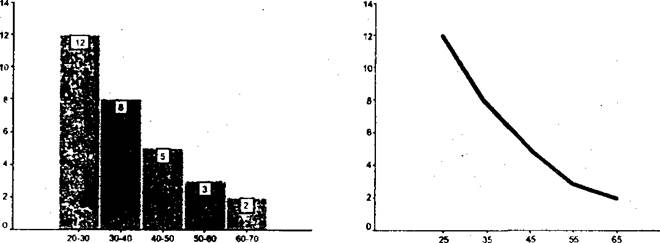
Возрастные группы Возрастные группы

Рис. 3. Гистограмма рас- Рис. 4. Полигон распределения

пределения возрастов возрастов

Построение таблиц и графиков — это первый шаг статистического анализа. Следующим шагом является оценка параметров распределения. Вычисляются показатели, которые позволяют дать еще более сжатое описание наблюдаемых значений.

Эти показатели распадаются на две основные группы:

1) меры центральной тенденции;

2) меры рассеяния.

1) К наиболее часто используемым показателям первого типа относится так называемое (арифметическое) среднее. Вычисляют его, как известно, путем суммирования значений всех наблюдений и деления полученной суммы на общее число наблюдений.

В случае сгруппированных данных поступают следующим образом: находят середину каждого интервала, это значение умножают на частоту, полученные величины складывают и делят на общее число наблюдений. Рассматриваемый показатель характеризует область распределения, в которой концентрируются наиболее типичные представители изучаемой выборки. Но это справедливо лишь для тех случаев, когда распределение близко к нормальному. При таком распределении основная масса значений концентрируется в его средней части, а любые отклонения встречаются тем реже, чем дальше они отстоят от центра. Например, распределение такого признака, как рост человека, в целом близко к нормальному: больше всего людей среднего роста, а очень высокие и очень маленькие по­падаются довольно редко. Средняя величина удобна для сравнения двух выборок или двух популяций. Так, мы говорим, что мужчины в среднем выше женщин, и это утверждение вполне справедливо несмотря на то, что встречаются высокие женщины, рост которых значительно превышает среднестатистический. Или, например, известно, что средний рост мужчины-пигмея меньше роста средней европейской женщины.

В таблице 8.2 показано, как вычислить средний возраст для выборки из 20 посетителей библиотеки. Заметьте, что каждое значение просто умножается на свою абсолютную частоту.

Приведенный нами пример (см. табл. 8.2) показывает, насколько среднее уязвимо для «крайних» значений. Фактически для нашей небольшой выборки молодых людей прибавление одного - восьмидесятилетнего - читателя заметно увеличило средний возраст. Степень «возмущения» среднего под влиянием единичных значений уменьшается в прямом соответствии с ростом объема выборки. Заметим также, что при расчете среднего для сгруппированных данных частоты умножаются на значение, соответствующее середине интервала группировки.

Две другие меры центральной тенденции — это мода (Мо) и медиана (Мd). В качестве моды берется значение, кото­рое чаще всего встречается в распределении. Моду специально вычислять не надо. Достаточно сгруппировать данные и выбрать тот класс, в который попадает больше всего наблюдений. В разобранном выше примере (Табл. 1) лучше всего представлена категория семейных людей. Это и есть мода для данной выборки. Встречаются распределения, имеющие не одну, а две моды. Распределение такого типа называется бимодальным. На графике в этом случае мы увидим две вершины. Чаще всего это указывает на то, что выборка является неоднородной: в ней присутствуют два типа объектов. Констатация такого факта обычно наводит нас на мысль разбить всю выборку на две подгруппы и рассмотреть их отдельно.

Для того чтобы найти медиану, нужно ранжировать все наблюдения, то есть расположить их в порядке возрастания значений. Значение того наблюдения, которое окажется как раз посредине, и будет медианой. А если число наблюдений четное? Тогда сравнивают значения двух наблюдений, попадающих в середину. Если они различаются между собой, то берется их среднее арифметическое значение. В случае сгруппированных данных медиана рассчитывается по специальной формуле.

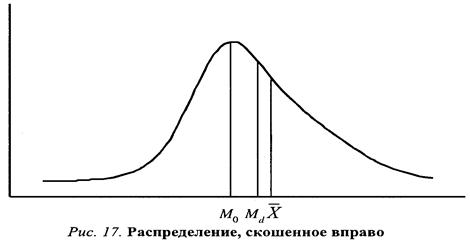
Когда распределение имеет нормальный вид (то есть оно симметрично), его среднее арифметическое значение и медиана совпадают. Когда же распределение асимметрично (скошено), медиана лучше схватывает его центральную тенденцию. Выбор подходящей меры центральной тенденции определяется как характером распределения, так и характером используемых данных.

Качественные данные (шкала наименований) допускают использование только моды. Для ранжированных данных (шкала порядка) допустимо использование и моды, и медианы. Количественные данные (шкала равных интервалов) можно описывать любым из трех показателей, хотя на практике чаще всего в этом случае вычисляют среднее арифметическое значение. Именно этот показатель вместе с показателем рассеяния участвует в расчете целого ряда других статистических показателей.

2) Показатели рассеяния характеризуют степень разброса данных вокруг некоторого среднего значения. Мы говорим о значительном рассеянии тогда, когда многие значения сильно отклоняются от воображаемого центра распределения. Специалисты по математической статистике говорят, что в этом случае данные «размазаны». Про распределение, характеризующееся малым разбросом, говорят, пользуясь аналогией из области стрельбы, что данные ложатся кучно. Понятно, что в первом случае среднее значение оказывается более информативным показателем, чем во втором случае, то есть оно лучше описывает выборку в целом. Например, в кордебалет идет строгий отбор танцовщиц по росту. В результате рассеяние показателей роста в этой группе людей значительно меньше, чем по популяции в целом. Зная средний рост балерины, можно быть уверенным, что реальный рост любой балерины будет очень близок к нему.

Как оценить степень рассеяния значений переменной? Здесь тоже существуют разные способы, выбор которых в каждом конкретном случае определяется характером данных — их типом и распределением. Некоторое представление о рассеянии мы получаем, когда рассматриваем крайние члены распределения. Расстояние между ними называется размахом.

Например, в разобранном выше примере (Табл. 2) выборка включает индивидов, чей возраст колеблется в пределах от двадцати до семидесяти лет. Общий размах составляет пятьдесят лет. Большинство людей (40 %) моложе тридцати лет. Но в выборку попали два человека, которым уже за шестьдесят. Если мы вычислим показатель центральной тенденции по формуле среднего арифметического, то получим значение 36,5. Так как распределение сильно скошено, этот показатель сильно отличается от моды (Mo=25 лет). Медиана в этом случае лежит между этими двумя значениями (Md=33,3).

Для более точной оценки рассеяния в случае измерений по шкале равных интервалов используется показатель, называемый дисперсия. В этом случае учитывается отклонение каждого индивидуального значения от среднего в одну или в другую сторону. Нас интересует сумма таких отклонений. Но в случае симметричного распределения эта сумма всегда обращается в нуль, поскольку положительные и отрицательные отклонения взаимно гасятся. Сумма квадратов отклонений от среднего, деленная на количество наблюдений дает значение дисперсии.

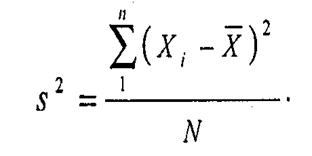
Для того чтобы вычислить значение дисперсии, нужно вычесть из каждого наблюдаемого значения среднее, возвести в квадрат все полученные отклонения, сложить квадраты отклонений и разделить полученную сумму на объем выборки.

Если извлечь из дисперсии квадратный корень, то мы получим еще одну меру рассеяния — стандартное отклонение (Sx), которое также называют среднеквадратическим отклонением. Удобство этого показателя в том, что он выра­жается в тех же единицах, что и сами измеренные ве­личины:

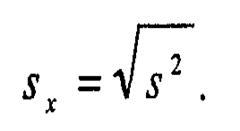
Рассмотренный показатель очень удобен, когда форма распределения близка к той, которая называется нормальным распределением.

Мы уже упоминали этот термин. Сейчас поясним, что он означает. Нормальное распределение — это такое распределение непрерывного признака, которое симметрично относительно среднего значения и если откладывать его значения на графике, то кривая имеет вид колокола. Рост человека оказывается одним из признаков, обнаруживающих распределение, хорошо описываемое нормальной кривой. Если мы измеряем рост многих людей, например — призывников в армию, а затем на основе этих данных строим график, то мы получаем нормальную кривую. С точки зрения анализа данных нормальное распределение привлекательно тем, что его можно исчерпывающе описать через два параметра — значение среднего и стандартного отклонения (дисперсии). Вместо тысяч значений — всего два числа. Чрезвычайно эффективный метод сжатия информации.

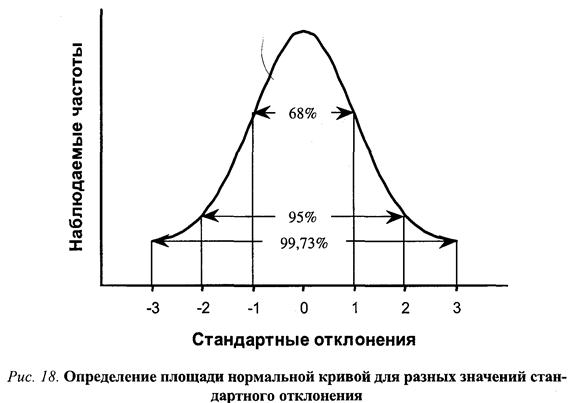
Стандартное отклонение действительно позволяет четко задавать критерии для выявления статистической нормы. Это возможно благодаря тому, что свойства нормального распределения хорошо известны и достаточно просто описываются. Так, известно, что в диапазоне одного стандартного отклонения в обе стороны от среднего оказывается примерно 68 % всех наблюдений, а если взять два стандартных отклонения, то этот участок распределения покроет около 95 % всех случаев. Значит, за этот диапазон выходит всего 5% возможных наблюдений.

Проинтерпретируем это содержательно. Что значит «высокий человек»? С точки зрения статистики человек, рост которого превышает средний рост по данной популяции более чем на величину одного стандартного отклонения, может считаться высоким. А того, чей рост выделяется в положительную сторону более чем на два стандартных отклонения, следует отнести к категории очень высоких. Ведь такой рост будет встречаться не чаще, чем в трех случаях из ста.

Используя свойства нормального распределения, можно ввести строгие количественные критерии, определяющие, что такое «нормальный вес», «нормальная острота зрения» и т. д. Психологические тесты тоже создаются с опорой на эти статистические закономерности. Нормы для оценки результатов испытаний выводят эмпирически с использованием аппарата математической статистики, т.е. трудность заданий подбирается таким образом, чтобы распределение результатов решения тестовых задач (число правильных ответов) описывалось нормальным законом. А затем строится шкала, где среднему значению соответствует сто баллов, а стандартное отклонение равно пятнадцати баллам. Выводимый показатель называется коэффициентом интеллектуального развития (по-английски — intelligence quotient, или сокращенно IQ). Человек, у которого этот показатель ниже 70, считается умственно отсталым, а человека с показателем выше 130 относят к категории особо умственно одаренных.

Мы подробно разобрали случай, когда анализиру­ется характер распределения одной переменной. Эти приемы очень важны, поскольку на них основаны все другие виды статистического анализа.

3.2. ДВУМЕРНЫЙ АНАЛИЗ

Теперь мы можем перейти к более сложному виду анализа, каким является двумерный анализ. Здесь рассматривается связь между двумя переменными. Мы имеем пары наблюдений, полученные на одном объекте. Это могут быть, например, результаты по двум тестам. Нас интересует, как один изучаемый признак связан с другим.

Таблица 8.3 Взаимосвязь между уровнем образования и занятиями физкультурой

	Уровень образования	Всего
Низкий	Высокий
Делают зарядку	50	200
Не делают зарядку	205	45
Всего

В таблице 8.3 два столбца (для образования) и две строки (для занятий физкультурой), следовательно, размерность этой таблицы 2х2. Кроме того, имеются дополнительные крайний столбец и крайняя строка (маргиналы таблицы), указывающие общее количество наблюдений в данной строке или в столбце. В правом нижнем углу указана общая сумма, т. е. общее число наблюдений в выборке. Не давшие ответа уже исключены (для реальных данных их число также стоит указать, но не в таблице, а в подтабличной сноске).

Заметим здесь, что многие исследователи при построении таких таблиц пользуются неписаным правилом: для той переменной, которую полагают независимой, отводится верхняя строка (горизонталь), а зависимую располагают «сбоку», по вертикали (разумеется, соблюдение этого правила не является обязательным и ничего с точки зрения анализа не меняет).

Обычно характер взаимоотношений между переменными в небольшой таблице можно определить даже «на глазок», сравнивая числа в столбцах или строках. Еще легче это сделать, если вместо абсолютных значений стоят проценты. Чтобы перевести абсолютные частоты, указанные в клетках таблицы, в проценты, нужно разделить их на маргинальные частоты и умножить на 100. Если делить на маргинал столбца, мы получим процент по столбцу.

Например, 50/255х100 = 19,6%, т. е. 19,6% имеющих низкий уровень образования делают зарядку (но не наоборот!). Если делить на маргинал строки, то мы получим другую величину - процент по строке. В частности, можно заметить, что 80% делающих зарядку, составляют люди с высоким уровнем образования(200/250х100). Деление на общую численность выборки дает общий процент. Так, всего в выборке 50% людей, делающих зарядку.

Так как вывод о наличии взаимосвязи между переменными требует демонстрации различий между подгруппами по уровню зависимой переменной, при анализе таблицы сопряженности можно руководствоваться простыми правилами. Во-первых, нужно определить независимую переменную и, в соответствии с принятым определением, пересчитать абсолютные частоты в проценты. Если независимая переменная расположена по горизонтали таблицы, мы считаем проценты по столбцу; если независимая переменная расположена по вертикали, проценты берутся от сумм по строке. Далее сравниваются процентные показатели, полученные для подгрупп с разным уровнем независимой переменной, каждый раз внутри одной категории зависимой переменной (например, внутри категории делающих зарядку). Обнаруженные различия свидетельствуют о существовании взаимосвязи между двумя переменными.

Элементарная таблица сопряженности размерности 2х2 - это минимально необходимое условие для вывода о наличии взаимосвязи двух переменных.

Знания о распределении зависимой переменной недостаточно. Нельзя, например, утверждать, будто из того, что 75% детей-первенцев имеют интеллект выше среднего, а 25% - средний и более низкий, следует зависимость между порядком рождения и интеллектом. Необходимо проанализировать и распределение показателей интеллекта для детей-непервенцев. Варьировать должна не только зависимая, но и независимая переменная.

Таблица 8.4 Oбщая форма таблицы сопряженности размерности 2х2

	Переменная Х	Всего
Переменная У		а	б	А+б
	с	д	С+д
Всего	А+с	Б+д	n

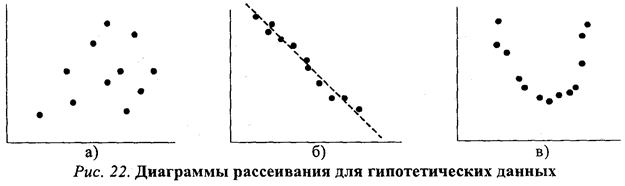
Между переменными Х и Y существует линейное отношение: если одна переменная возрастает по величине, то это же происходит и с другой. Очевидно, что чем более компактно, «скученно» располагаются точки-наблюдения вокруг пунктирной прямой линии (описывающей идеальное линейное отношение Х и Y), тем сильнее зависимость. На рисунке 22 приведены три диаграммы рассеивания.

Очевидно, что на рисунке 22а какая-либо связь между x и y попросту отсутствует. На рисунке 22б воображаемая прямая линия (отмечена пунктиром) пересекла бы диаграмму сверху вниз, из левого верхнего в правый нижний угол. Иными словами, линейная связь в этом случае имеет обратное направление: чем больше X, тем меньше зависимая переменная У.

Заметим также, что «кучность» расположения точек вдоль воображаемой прямой на рисунке 22б не очень велика, а значит и связь (корреляция) между переменными не только обратная, отрицательная, но еще и не очень сильная, умеренная.

Наконец, на рисунке 22в зависимую и независимую переменную связывает явно нелинейное отношение: воображаемый график нисколько не похож на прямую линию и напоминает скорее параболу.

Методы анализа, о которых сейчас пойдет речь, не годятся для этого нелинейного случая, так как обычная формула для подсчета коэффициента корреляции даст нулевое значение, хотя связь между переменными существует.

Существует обобщенный показатель, позволяющий оценить, насколько связь между переменными приближается к линейному функциональному отношению, которое на диаграмме рассеивания выглядит как прямая линия. Это коэффициент корреляции, измеряющий тесноту связи между переменными, т. е. их тенденцию изменяться совместно. Как и в рассмотренных выше мерах связи качественных признаков, коэффициент корреляции позволяет оценить возможность предсказания значений зависимой переменной по значениям независимой.

Само слово «корреляция» как раз и означает «взаимосвязь». Какого типа отношения возможны между двумя переменными? Ну, во-первых, признаки могут быть совершенно независимыми друг от друга. Тогда изменения одного никак не связаны с изменением другого. Мы говорим, что переменные не коррелированны между собой. Если признаки связаны, то сама связь может быть прямой или обратной.

В первом случае большим значениям одного признака соответствуют более высокие значения другого и наоборот.

Во втором случае увеличение первого признака сопровождается уменьшением второго, а уменьшение первого — увеличением второго. Статистики говорят о положительной и отрицательной корреляции. Наконец, степень связи тоже может варьироваться от максимума, когда значения одного признака позволяют уверенно предсказывать значения другого, до ее полного отсутствия. Коэффициент корреляции отражает всю гамму возможных отношений. Его значение может варьироваться от +1 до — 1. Положительные значения указывают на прямую связь между переменными, отрицательные — на обратную. Нуль соответствует случаю отсутствия корреляции.

Пример. Предположим, что у многих людей измеряют рост и вес тела. Каждый человек описывается двумя показателями, и в результате образуются два ряда измерений. Сравнивая между собой пары измерений, мы стремимся выявить характер связи между переменными. Между ростом и весом тела существует довольно высокая положительная корреляция. Это значит, что высокий человек, как правило, весит больше, чем человек меньшего роста. Связь эта не однозначная: высокий человек может быть очень худым, а человек невысокого роста может быть очень полным. Поэтому значение коэффициента корреляции в данном случае находится где-то между 0 и +1, видимо, чуть ближе к единице.

Коэффициент корреляции по-разному вычисляется для измеренных показателей (рост, вес) и для ранжированных данных (оценки, предпочтения). Но его окончательная форма и интерпретация остаются теми же. Если данные носят качественный характер (мужчина — женщина, совершеннолетний — несовершеннолетний, работающий — пенсионер), то вместо коэффициента корреляции применяются другие меры связи, основанные на сравнении частот. Для тех случаев, когда два ряда получены с помощью разных шкал, имеются свои вычислительные процедуры. Но общая логика анализа сохраняется.

Следует специально остановиться на вопросе интерпретации данных двумерного анализа, поскольку здесь требуется известная осторожность. Сам факт наличия связи двух переменных еще не позволяет утверждать существование причинно-следственных отношений между ними. Корреляция может указывать на такие отношения, но одной этой информации недостаточно, чтобы делать однозначные выводы.

Итак, в ряде случаев корреляция между двумя переменными отражает то обстоятельство, что они связаны между собой, как причина и следствие. Но причинно-следственные отношения — это лишь один из возможных типов связи. Определенно можно утверждать только следующее: если два явления никак не связаны между собой, то заведомо исключены любые взаимовлияния. Отсутствие корреляции опровергает гипотезу о возможных связях причинно-следственного характера, и такой отрицательный результат может быть полезен в плане уточнения теории.

Отношения между двумя коррелированными переменными X и Y могут быть содержательно самыми разными:

Случай 1: явление X вызывает явление Y, выступает как его причина.

Случай 2: явления X и Y взаимно обусловливают друг друга.

Случай 3: некоторое третье явление А вызывает явление X и явление Y, выступает как причина их обоих.

Случай 4: явление X вызывает явление Y, действуя в комплексе с другими факторами.

Для иллюстрации приведем пример. Он похож на шутку, но хорошо демонстрирует суть проблемы. Если сравнивать между собой два показателя — потребление мороженого и количество утонувших, то между ними можно обнаружить положительную корреляцию. Значит ли это, что любовь к мороженому приводит к несчастным случаям на воде или (совершенно абсурдный вывод) что отношение здесь обратное? Конечно, нет. Очевидно, что есть некий третий фактор, который объясняет оба явления. Это — температура воздуха. В жаркую погоду едят много мороженого и купаются. В холодную погоду потребление мороженого и количество купающихся резко падает. Понятно, что в эти дни почти никто не тонет. Перед нами ситуация, соответствующая третьему из схематически представленных случаев.

Социальные науки чаще всего имеют дело с явлениями, которые отличаются множественной детерминацией и контекстуальным характером. Здесь трудно устранить влияние посторонних переменных, выделить явление в чистом виде. Поэтому необходима особая тщательность в интерпретации наблюдаемых фактов.

Корреляционный анализ представляет собой метод выявления связи между двумя переменными. Если число переменных больше двух, то можно, вообще говоря, рассматривать каждую пару отдельно.

Но существуют приемы, специально разработанные для данных такого рода, которые в совокупности носят название многомерный анализ. Мы рассмотрим один из этих методов — факторный анализ, который довольно часто используется в социальных исследованиях. В вычислительном плане он весьма сложен, но использование компьютера существенно упрощает дело. Современному исследователю не надо вдаваться в тонкости вычислительной процедуры, а достаточно понимать возможности этого метода и знать особенности работы с ним.

Факторный анализ является своеобразным развитием метода множественных корреляций. Вначале рассчитываются коэффициенты корреляции между парами переменных. Затем чисто математически получают несколько общих факторов, связанных с группами изучаемых признаков. Поскольку число таких факторов меньше числа исходных переменных, этот вид анализа можно рассматривать как способ сжатия информации, приведения ее к более компактному виду. Последний этап анализа — содержательная интерпретация полученных факторов. Ее осуществляет сам исследователь, выявляя те переменные (признаки), которые теснее всего связаны с каждым фактором.

Например, исследуются интересы людей. Если вокруг одного фактора группируются такие виды активности, как посещение театра, концертов, художественных выставок, то мы назовем такой фактор «эстетические интересы». Другим фактором может быть, например, интерес к спорту. В результате мы получаем несколько групп однотипных интересов. С точки зрения структуры данных отдельный фактор представляет собой как бы интегральный индикатор, выявляющий комплекс взаимосвязанных проявлений.

Еще один пример. Исследование качества обслуживания в доме престарелых путем опроса его обитателей выявило два главных фактора удовлетворенности: отношение персонала (доброта, отзывчивость, уважение, готовность помочь, расторопность) и условия содержания (состояние здания и территории, оборудование комнат, чистота, качество питания).

Итак, факторный анализ является объективным методом выявления структуры изучаемых данных. Его можно рассматривать как количественный аналог типологического анализа, проводимого на качественном уровне. Будучи формальным аппаратом, факторный анализ не может гарантировать, что получаемые результаты будут интересными, с точки зрения исследователя. Например, иногда выделяемые факторы трудно содержательно интерпретировать: в них входят довольно разнородные компоненты, которые трудно объединить каким-то общим понятием. Во всяком случае, как любой метод вообще, факторный анализ сам по себе не может быть хорошим или плохим, эффективным или бесполезным. Все зависит от того, насколько уместно он применяется, в какой степени он соответствует задачам исследования и характеру анализируемых данных.

Рассмотрим вторую большую группу количественных методов анализа, на основе которых делается статистический вывод. В этом случае стоит задача перехода от отдельной выборки к характеристикам (параметрам) генеральной совокупности, то есть всего класса объектов в целом. Дело в том, что исследователь редко имеет возможность изучать всех представителей какой-то группы или социальной категории. Можно, например, обследовать все многодетные семьи, проживающие в данном микрорайоне. Но тогда выводы в полной мере будут относиться лишь к этой конкретной группе людей. Насколько они справедливы для многодетных семей всего города или области? Чтобы ответить на этот вопрос, нужно знать, насколько типична или специфична обследованная группа. Если она типична, то сходные проблемы выявятся и у других многодетных семей. Если группа очень специфична, то мы не имеем права обобщать полученные данные. На языке статистики это значит, что наша выборка принадлежит к другой генеральной совокупности. Опять мы сталкиваемся с задачей сравнения характеристик выборки и генеральной совокупности, с необходимостью суждения об их тождестве или различии.

В реальной практике исследования вопрос чаще всего ставится несколько иначе, но логически он относится к тому же классу. Требуется сравнить две группы (выборки) и решить, насколько значимо они различаются между собой. Любой эксперимент предполагает оценку эффекта изучаемого воздействия. Исследователь в этом случае стремится показать, что экспериментальная группа существенно отличается в интересующем его отношении от контрольной группы. Оценивая эффективность образовательных программ, лечебных и оздоровительных мероприятий, мы смотрим, насколько существенными оказываются позитивные сдвиги. И что называть сдвигом? Если больной выздоровел, то это — явный качественный сдвиг. Если ему стало легче, его меньше беспокоят боли, то это некоторый количественный сдвиг. Но можно ли говорить о переходе из одного состояния в другое? Для этого нам нужны критерии тождества или различия двух состояний. Статистика предлагает определенные формальные правила, позволяющие делать такого рода выводы.

Общая логика рассуждений такова. У нас есть два множества объектов. Если различие между ними по какому-то параметру настолько очевидное, что эти два множества не пересекаются, мы с уверенностью говорим, что это два разных класса объектов. Например, если минимальное значение дохода в одной группе на­селения превышает максимальное значение дохода в другой группе, то мы вправе утверждать, что группы различаются по своему материальному положению. Но это случай весьма тривиальный. Никому не придет в голову проводить исследования, чтобы доказать, что слон больше муравья. Это очевидно. Наука имеет дело с нетривиальными задачами, то есть с такими ситуациями, где на основании имеющихся знаний мы выдвигаем какие-то более или менее правдоподобные гипотезы, которые еще нуждаются в проверке и в доказательстве. Обычный случай, с которым имеет дело ученый, — это частично пересекающиеся множества (частично перекрывающиеся распределения). Вот тут и встает проблема различения и отождествления.

Проблема осложняется тем, что, кроме нечеткости категорий (математики в этом случае говорят о размытых множествах), нужно учитывать возможность всякого рода ошибок. Ошибки измерений связаны с точностью тех инструментов, которые мы используем. Никакой инструмент не дает абсолютной точности измерений. А надежность тех методов сбора информации, которыми пользуются исследователи в социальных науках, далеко уступает надежности физических приборов. Кроме того, нужно учитывать возможную ошибку выборки. Так как для исследования берутся только некоторые экземпляры, у нас нет никакой гарантии, что они являются типичными представителями популяции в целом. Рассмотренные нами ранее способы корректного построения выборки направлены на устранение систематической ошибки. Но случайные ошибки полностью исключить невозможно. Статистика ставит перед собой задачу: оценить степень надежности получаемых данных и степень надежности тех выводов, которые делаются на их основе. Для этой цели используется аппарат теории вероятностей.

Нетрудно доказать, что ошибка выборки зависит от двух моментов: от размера выборки и от степени вариации признака, который нас интересует. Чем больше выборка, тем меньше вероятность того, что в нее попадут индивиды с крайними значениями исследуемой переменной. С другой стороны, чем меньше степень вариации признака, тем в целом ближе будет каждое значение к истинному среднему. Размер выборки нам известен. А степень вариации признака можно примерно оценить по степени разброса данных. Таким образом, зная размер выборки и получив меру рассеяния наблюдений, нетрудно вывести показатель, который называется стандартная ошибка среднего. Он дает нам интервал, в котором должна лежать истинная средняя популяции.

Описанная процедура основана на том факте, что ошибки выборки и ошибки измерений вообще подчиняются нормальному закону, поскольку они обуслов­лены множеством случайных факторов. При этом совершенно не обязательно, чтобы само распределение данных имело нормальный вид. Представим себе, что мы изучаем разные случайные выборки из одной генеральной совокупности. Оценки среднего, получаемые в каждом случае, будут несколько различаться между собой, но в целом они будут группироваться вокруг истинного значения. Если построить распределение этих оценок, то оно окажется нормальным. В центре его будет лежать среднее по генеральной совокупности, а стандартное отклонение будет равно стандартной ошибке среднего. Но последний показатель, как мы видели, можно вывести и на основании одной выборки, вычисляя по формуле: стандартная ошибка = стандартное отклонение, деленное на корень квадратный из числа наблюдений. Теперь, зная свойства нормального распределе­ния, можно указать интервал, в котором должно находиться истинное среднее. Выше, рассматривая свойства нормального распределения, мы отмечали, что в диапазоне двух стандартных отклонений в обе стороны от среднего сосредоточено примерно 95 % всех случаев. Значит, вероятность получить значение, выходящее за эти пределы, не превышает 5 %, то есть такие ошибки будут встречаться не чаще, чем один раз из 20 случаев. С вероятностью 0,95 можно утверждать, что истинное значение лежит в указанных границах, которые задают доверительный интервал.

Итак, поскольку какая-то вероятность ошибки всегда присутствует, мы вводим количественную меру надежности наших выводов. Все статистические критерии построены по этому принципу. Уровень 95 % принят как соответствующий достаточной надежности суждений. Если мы стремимся к еще большей надеж­ности, то можно взять 99 % уровень. Это означает, что случайная ошибка допускается не чаще, чем в одном случае из ста. Точные доверительные границы для 95 % уровня составляют ±1,96 стандартной ошибки среднего, а для 99 % уровня мы используем коэффициент 2,58. В первом случае вне этого интервала остается не более 5 % возможных значений (по 2,5 % с каждой стороны). Во втором случае — не больше 1 % (по 0,5 % с каждой стороны). Рассмотрим пример. Допустим, что в некоторой группе безработных из 25 человек средний возраст оказался 32 года. А массовые исследования говорят, что средний возраст для этой категории составляет 40 лет, а стандартное отклонение составляет 6 лет. Нас интересует вопрос, типична или нетипична наша выборка. Если это перевести на язык статистики, то мы спрашиваем, можно ли объяснить различие средних ошибкой выборки.

Статистический вывод представляет собой процесс проверки гипотез. Причем первоначально всегда выдвигается предположение, что наблюдаемые различия носят случайный характер, то есть выборка принадлежит к той же генеральной совокупности. В статистике такое предположение получило название нулевая гипотеза. Итак, мы полагаем для начала, что наша выборка вполне типична. А затем мы спрашиваем: Какова вероятность получить выборку с таким средним (32 года) из генеральной совокупности, средний возраст которой нам известен (40 лет)? Мы знаем, что при многократных испытаниях получаемые значения будут распределены нормально, и средняя этого распределения будет равна 40 годам. Стандартную ошибку при условии, что мы будем каждый раз брать по 25 человек, можно рассчитать по известной нам формуле: мы делим 6 (стандартное отклонение) на корень квадратный из 25 и получаем значение 1,2 года (стандартная ошибка среднего). Затем вычисляется доверительный интервал, который в нашем случае при уровне достоверности в 95 % составит:

40 + 1,96 - 1,2 года = 40 ± 2,35 года (т. е. от 37, 65 до 42, 35)

Значение среднего для нашей выборки (32) лежит вне найденного диапазона. Это может означать, что:

а) либо мы наткнулись на тот чрезвычайно редкий
случай, который лежит на самом краю распределения;

б) либо наше предположение, что два средних (по
выборке и по генеральной совокупности) не различаются, ошибочно.

Если основываться только на имеющихся данных, то мы имеем основание отклонить нулевую гипотезу, то есть считать, что наша группа какая-то особая. Мы говорим, что различие между средними статистически значимо на уровне р < 0,05. Вероятность ошибки составляет менее 5 %, и поэтому мы с достаточной уве­ренностью утверждаем, что различие не случайно. Если мы задаем более строгий критерий (99 %), то у нас еще больше оснований отклонить нулевую гипотезу. Мы говорим тогда, что различие статистически высоко значимо. Для социальных исследований 95 % уровень значимости считается вполне приемлемым.

Разобранный пример иллюстрирует случай сравнения эмпирического и теоретического распределения. Аналогичная процедура применяется и тогда, когда требуется оценить различие двух выборок. Мы исходим из допущения, что наблюдаемое различие средних обусловлено случайными факторами (ошибкой выборки и измерения). Другими словами, мы предполагаем, что обе выборки принадлежат к одной генеральной совокупности, параметры которой нам неизвестны. Затем мы оцениваем различие средних с учетом наблюдаемого рассеяния данных в каждой из выборок. Критические значения задаются с учетом выбранного уровня значимости. Если заданная величина оказывается превышенной, мы отвергаем нулевую гипотезу и считаем, что наблюдаемые различия не случайны.

Мы разобрали принципы проверки статистических гипотез. Существуют разные статистические критерии, разработанные для разных типов данных. Некоторые из них, так называемые параметрические критерии, применимы только к данным, полученным с помо­щью интервальных шкал. Название отражает тот момент, что в основе процедуры оценки лежит предположение о характере распределения данных. Если эти условия не выполняются, то выводы оказываются сомнительными. К наиболее известным критериям этого типа относится критерий Стьюдента, применяемый для оценки различия средних. Но разработан также целый ряд статистических процедур, которые не привязаны к какому-то определенному распределению. Эти критерии, которые называются непараметричекими, особенно удобны для анализа данных, с которыми обычно имеют дело социальные науки. Примером может случить критерий хи-квадрат, который основан на сравнении частот. Кстати, этот же метод используется для оценки связи между качественными признаками. Выбор подходящего критерия — задача весьма непростая. Здесь следует обратиться к помощи специалиста по математической статистике.

Нужно помнить, что грамотное применение статистики требует от исследователя специальной подготовки. Но это касается и приемов качественного анализа, и методов сбора данных. По методам обработки социальной информации имеется обширная литература — от элементарных учебников до серьезных руководств.