СИ с мультипликативной погрешностью

Эта погрешность связана со случайными изменениями наклона функции преобразования. В этом случае сигнал на выходе СИ имеет вид: 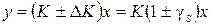, где 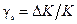- относительная мультипликативная погрешность.

Найдём ширину полосы неопределённости в этом случае. При фиксированном значении выходного сигнала y, вследствие неопределенности D K значения K, это значение y реализуется при двух значениях х: 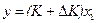и 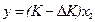. Отсюда найдем , .

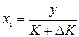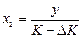Тогда ширина полосы неопределенности .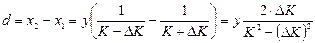

Будем считать, что 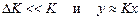. Тогда 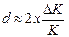, и относительная мультипликативная погрешность 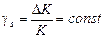(см. рис.).

Относительная мультипликативная погрешность остаётся постоянной при любых x, но такой идеальный случай практически не осуществим, т.к. нет СИ без аддитивных погрешностей.