2014-02-13
732
Рассмотрим погрешность, определяемую формулой (13) предыдущего раздела:
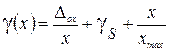. (1) Эту формулу называют трёхчленной формулой. Если измеряемая величина х мала, так что 
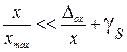, последним слагаемым можно пренебречь по сравнению с остальными и формула статической погрешности примет вид
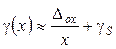.(2). Формула (2) описывает погрешность прибора с полосой погрешности вида III, эту формулу называют двучленной. Обычно эту формулу записывают в другом виде, исходя из следующих соображений.
Оказывается, что легче всего измерять погрешность СИ в начале шкалы (при х =0) и в конце шкалы (при x» x k). В первом случае, поскольку в начале шкалы, т.е. при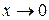 
, погрешность
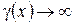. Поэтому относительную погрешность прибора описывают приведенной погрешностью прибора
.
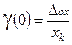В конце шкалы, т.е. при x» x k, из (2) имеем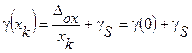 
. Используя эти результаты, формулу (2) представим в виде:
.
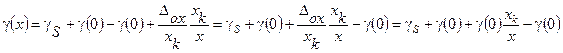Т.о. двучленная формула принимает следующий вид: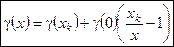 
.
Эта формула справедлива для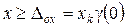 
. При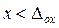 
ей пользоваться нельзя.
По ГОСТу обозначение класса прибора с двучленной формулой основной погрешности даётся в виде отношения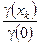 
, где числитель и знаменатель (их не делят друг на друга !!) выражают в процентах.
|
|
|
Для приборов, у которых основной погрешностью является аддитивная погрешность (сдвиг нуля), т.е.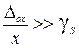 
, мультипликативной погрешностью пренебрегают. В этом случае из формулы (2) следует: 
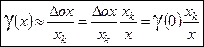, т.е. для приборов, у которых основной погрешностью является аддитивная погрешность, формула расчета погрешности оказывается одночленной. В качестве класса точности приборов с такой погрешностью даётся значение 
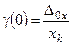, выраженное в %.
