Частотные характеристики фильтров

Пример.

Передаточная функция фильтра рис. 6.1: H(z) = b₀/(1-a₁z). При а₁= 0.5 полюс знаменателя: z_р= 2. |z_р|>1. Фильтр устойчив.

Передаточная функция фильтра рис. 6.2: H(z) = b₀/(1+a₁z). При а₁= 1.1 полюс знаменателя: z_р= -0.909. |z_р| < 1. Фильтр неустойчив, что и подтверждает пример фильтрации.

Передаточная функция фильтра рис. 6.3: H(z) = 0.5(1+z)/(1-z). Полюс знаменателя: z_р= 1. В принципе, фильтр неустойчив, но эта неустойчивость проявляется только при k = ∞. Импульсный отклик фильтра h(n) = {0.5,1,1,1, ….}, сумма которого равна ∞ только при n = ∞, т.е. при интегрировании бесконечно больших массивов. При интегрировании конечных массивов результат всегда конечен.

Приведенный критерий устойчивости относится к несократимой дроби, т.к. в противном случае возможна компенсация полюса нулем передаточной функции, и следует проверить наличие однозначных нулей и полюсов.

Проверка на устойчивость требуется только для рекурсивных цифровых фильтров (систем с обратной связью), нерекурсивные системы всегда устойчивы.

Общие понятия. От z-образов сигналов и передаточных функций подстановкой z = exp(-jwDt) в уравнение (8.2) можно перейти к Фурье-образам функций, т.е. к частотным спектрам сигналов и частотной характеристике фильтров, а точнее – к функциям их спектральных плотностей.

Можно применить и способ получения частотных характеристик непосредственно из разностного уравнения системы обработки данных. Так как цифровая фильтрация относится к числу линейных операций, то, принимая для сигнала на входе фильтра выражение x(kDt) = B(w) exp(jwkDt), мы вправе ожидать на выходе фильтра сигнал y(kDt) = A(w) exp(jwkDt). Подставляя эти выражения в разностное уравнение фильтра (4.1), получаем:

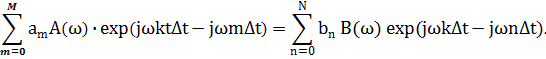
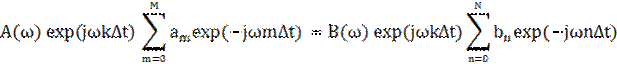
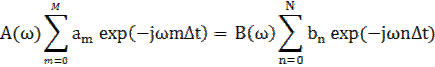(9.1)

Передаточная частотная функция (частотная характеристика при а_о=1):

(9.2)

Нетрудно убедиться, что полученная частотная характеристика пов- торяет функцию (8.2) при z = exp(-jwDt), что и следовало ожидать. Аналогично z-преобразованию (8.7), частотная характеристика фильтра представляет собой Фурье-образ его импульсной реакции, и наоборот. При Dt = 1:

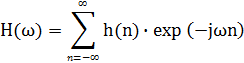(9.3)

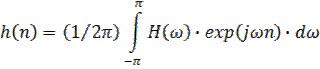(9.4)

В общем случае H(w) является комплексной функцией, модуль которой R(w) называется амплитудно-частотной характеристикой (АЧХ), а аргумент j(w) - фазочастотной характеристикой (ФЧХ).

A(w) = |H(w)| =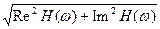

j(w) = arctg(-Im H(w)/Re H(w)).

На рис. 9.1 - 9.3 приведены частотные характеристики фильтров (модули и аргументы спектральных плотностей), которые были рассмотрены выше в примерах и на рис. 6.1 – 6.3. Графики приведены в границах главных диапазонов спектров, и получены непосредственной подстановкой z=exp(-jwDt) при Dt=1 в уравнения передаточных функций H(z).

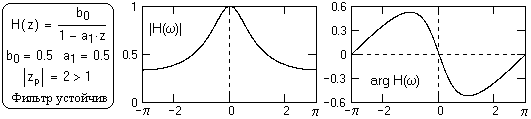
Рис. 9.1 Спектр не имеет особых точек.

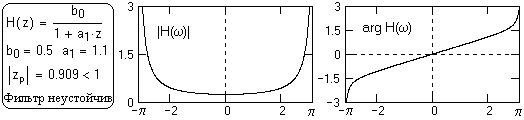
Рис. 9.2 Спектр имеет особые точки на границах диапазонов.

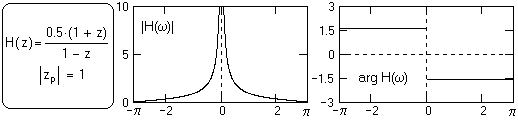
Рис. 9.3 Спектр интегрирующего фильтра. Особая точка на нулевой частоте.

При обработке ограниченных массивов амплитуда центрального пика равна количеству точек массива.

Основные свойства частотных характеристик фильтров:

1. Частотные характеристики являются непрерывными функциями частоты.

2. При дискретизации данных по интервалам Dt функция H(w) является периодической. Период функции H(w) равен частоте дискретизации входных данных F = 1/Dt. Первый низкочастотный период (по аргументу w от -p/Dt до p/Dt, по f от -1/2Dt до 1/2Dt) называется главным частотным диапазоном. Граничные частоты главного частотного диапазона соответствуют частоте Найквиста ±w_N, w_N= p/Dt. Частота Найквиста определяет предельную частоту обработки данных.

3. Для фильтров с вещественными коэффициентами импульсной реакции h(nDt) функция АЧХ является четной, а функция ФЧХ - нечетной. С учетом этого частотные характеристики фильтров обычно задаются только на интервале положительных частот 0-w_N главного частотного диапазона. Значения функций на интервале отрицательных частот являются комплексно сопряженными со значениями на интервале положительных частот.

Как правило, при частотном анализе фильтров значение Dt интервала дискретизации принимают за 1, что соответственно определяет задание частотных характеристик на интервале (0,p) по частоте w или (0,1/2) по f. При использовании быстрых преобразований Фурье (БПФ) вычисления спектров осуществляются в одностороннем варианте положительных частот в частотном интервале от 0 до 2p (от 0 до 1 Гц), где комплексно сопряженная часть спектра главного диапазона (от -p до 0) занимает интервал от p до 2p (для ускорения вычислений используется принцип периодичности дискретных спектров). Заметим, что при выполнении БПФ количество точек спектра равно количеству точек входной функции, а, следовательно, отсчет на частоте 2p, комплексно сопряженный с отсчетом на частоте 0, отсутствует. При нумерации точек входной функции от 0 до N он принадлежит точке N+1 - начальной точке следующего периода, при этом шаг по частоте равен 2p/(N+1). Современное программное обеспечение БПФ допускает любое количество точек входной функции, при этом для нечетного значения N частоте p соответствует отсчет на точке (N+1)/2, не имеющий сопряженного отсчета, а при четном значении N отсутствует отчет на частоте p (она располагается между отсчетами k=N/2 и N/2 +1). Отсчетам с номерами k главного диапазона БПФ (за исключением точки k=0) соответствуют комплексно сопряженные отсчеты N+1-k (за исключением точки k=(N+1)/2 при нечетном N).

Фазовая и групповая задержка. Задержка сигналов во времени относится к характерной особенности каузальных систем в целом, а, следовательно, рекурсивных и односторонних нерекурсивных фильтров.

Фазовая задержка, это прямая характеристика временной задержки фильтром гармонических колебаний. При подаче на вход фильтра гармоники sin wt, сигнал на выходе каузального фильтра, без учета изменения его амплитуды, равен sin(wt-j), при этом:

sin(wt-j) = sin w(t-t_p), ωt-j = ω(t-t_p).

Отсюда, фазовая задержка t_p на частоте w равна:

t_p = j /ω. (9.5')

При распространении (9.5) в целом на спектральную передаточную функцию фильтра получаем:

t_p(w)= j(w) /ω. (9.5)

Постоянство значения t_p(w) в определенном частотном диапазоне обеспечивает для всех гармоник сигнала такое же соотношение их фазовых характеристик, какое было на входе системы, т.е. не изменяет формы сигнала, если его спектр полностью сосредоточен в этом частотном диапазоне, и значения АЧХ в этом диапазоне также имеют постоянное значение. Это условие является определяющим, например, для систем передачи данных, для сглаживающих и полосовых частотных фильтров.

Что касается каузальных фильтров, то они, как правило, имеют в рабочем диапазоне определенную зависимость значения t_p от частоты, которая характеризуется групповым временем задержки (ГВЗ).

Допустим, что сигнал на входе фильтра представляет собой сумму двух гармоник с близкими частотами:

s(t) = cos ω₁t + cos ω₂t.

Тождественная тригонометрическая запись:

s(t) = 2 cos[0.5(ω₁+ω₂)t] · cos[0.5(ω₁-ω₂)t].

Эта запись показывает, что сумму двух гармоник с частотами ω₁ и ω₂ можно рассматривать, как амплитудную модуляцию гармоники с частотой (ω₁+ω₂)/2 гармоникой с частотой (ω₁-ω₂)/2. При прохождении через фильтр каждая из гармоник ω₁и ω₂ может получить различную задержку, при этом сигнал на выходе фильтра, без учета амплитудных изменений:

s(t) = cos (ω₁t-j₁) + cos(ω₂t-j₂).

Тождественная запись:

s(t) = 2 cos[0.5((ω₁+ω₂)t-(j₁+j₂))] · cos[0.5((ω₁-ω₂)t-(j₁-j₂))].

Пульсацию колебаний выразим через групповую временную задержку t_g:

cos[0.5((ω₁-ω₂)t-(j₁-j₂))] = cos[0.5(ω₁-ω₂)·(t-t_g)].

Отсюда:

(ω₁-ω₂)·t_g = j₁-j₂.

t_g = (j₁-j₂)/(ω₁-ω₂) = Dj /Dω. (9.6)

При распространении этого выражения на непрерывную частотную характеристику фильтра:

t_g(ω)= dj(w)/dω. (9.7)

Для вычислений ГВЗ удобно использовать комплексный логарифм передаточной функции фильтра:

Ln(H(ω)) = ln |H(ω)| + j·j(ω), j(ω) = Im[Ln(H(ω)].