Сглаживающие фильтры и фильтры аппроксимации
Частотный анализ цифровых фильтров
Основной инструмент цифровой фильтрации данных и проектирования цифровых фильтров – частотный анализ (второй распространенный термин – спектральный анализ). Частотный анализ базируется на использовании периодических функций, в отличие от численных методов анализа и математической статистики, где предпочтение отдается полиномам. В качестве периодических используются преимущественно гармонические функции – синусы и косинусы. По-существу, спектральный состав сигналов – это тонкая внутренняя структура данных, которые несет сигнал, и которая практически скрыта в динамическом (графическом) представлении больших множеств данных даже для опытных обработчиков. Точно так же частотная характеристика цифрового фильтра – это его однозначный функциональный паспорт, полностью определяющий сущность преобразования фильтром входных данных.
Однако следует отметить, что хотя сущность фильтрации сигналов состоит именно в направленном изменении частотного состава данных, которые несет сигнал, тем не менее, у начинающих специалистов существует определенное эмоциональное противодействие частотному подходу и его роли в анализе данных. Преодолеть это противодействие можно только одним путем – на опыте убедиться в эффективности частотного подхода.
Рассмотрим несколько примеров частотного анализа фильтров применительно к известным способам обработки данных.
Предположим, что требуется осуществить сглаживание (регуляри- зацию, аппроксимацию) по методу наименьших квадратов (МНК) равномерного по аргументу массива данных.
Простейший способ аппроксимации по МНК произвольной функции s(t) - с помощью полинома первой степени, т.е. функции вида y(t) = A+Bt (метод скользящих средних). В качестве примера произведем расчет симметричного фильтра на (2N+1) точек с окном от -N до N.
Для определения коэффициентов полинома найдем минимум функции приближения (функцию остаточных ошибок). С учетом дискретности данных по точкам tn = nDt и принимая Dt = 1 для симметричного НЦФ с нумерацией отсчетов по n от центра окна фильтра (в системе координат фильтра), для функции остаточных ошибок имеем:
s(A,B) = 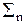 [sn - (A+B·n)]2.
[sn - (A+B·n)]2.
Дифференцируем функцию остаточных ошибок по аргументам 'А, В' и, приравнивая полученные уравнения нулю, формируем 2 нормальных уравнения:
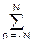 (sn-(A+B·n)) º
(sn-(A+B·n)) º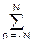 sn - A
sn - A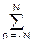 1 - B
1 - B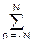 n = 0,
n = 0,
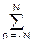 (sn-(A+B·n))·n º
(sn-(A+B·n))·n º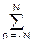 n×sn - A
n×sn - A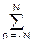 n - B
n - B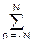 n2 = 0,
n2 = 0,
С учетом очевидного равенства 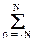 n = 0, результат решения данных уравнений относительно значений А и В:
n = 0, результат решения данных уравнений относительно значений А и В:
А = 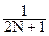
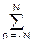 sn, B =
sn, B =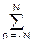 n×sn /
n×sn / 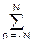 n2.
n2.
Подставляем значения коэффициентов в уравнение аппрокси- мирующего полинома, переходим в систему координат по точкам k массива y(k+t) = A+B·t, где отсчет t производится от точки k массива, против которой находится точка n = 0 фильтра, и получаем в общей форме уравнение фильтра аппроксимации:
y(k+t) = 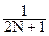
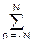 sk-n + t
sk-n + t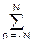 n×sk-n /
n×sk-n / 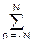 n2.
n2.
Для сглаживающего НЦФ вычисления производятся непосредственно для точки k в центре окна фильтра (t = 0), при этом:
yk = 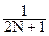
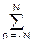 sk-n. (10.1.1)
sk-n. (10.1.1)
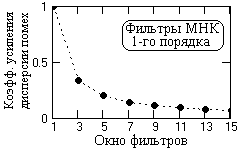 Рис. 10.1.1. Рис. 10.1.1. |
Импульсная реакция фильтра соответственно определяется (2N+1) значениями коэффициентов bn = 1/(2N+1). Так, для 5-ти точечного НЦФ:
h(n) = {0.2, 0.2, 0.2, 0.2, 0.2}.
Передаточная функция фильтра в z-области:
H(z) = 0.2(z-2+z-1+1+z1+z2).
Коэффициент усиления дисперсии шумов:
Kq = Sn h2(n) = 1/(2N+1),
т.е. обратно пропорционален ширине окна фильтра. Зависимость значения Kq от ширины окна приведена на рис. 10.1.1.
Частотная характеристика фильтра (передаточная функция фильтра в частотной области) находится преобразованием Фурье импульсной реакции h(n) (фильтр симметричный, начало координат в центре фильтра) или подстановкой z = exp(-jw) в выражение передаточной функции H(z). И в том, и в другом случае получаем:
H(w) = 0.2[exp(2jw)+exp(jw)+1+exp(-jw)+exp(-2jw)]. (10.1.2)
Можно использовать и непосредственно уравнение фильтра, в данном случае уравнение (10.1.1). Подадим на вход фильтра гармонический сигнал вида sk = exp(jwk). Так как сигнальная функция относится к числу собственных, на выходе фильтра будем иметь сигнал yk = H(w)exp(jwk). Подставляя выражения входного и выходного сигналов в уравнение (10.1.1), получаем:
H(w) exp(jwk) = 0.2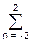 exp(jw(k-n))= 0.2 exp(jwk)
exp(jw(k-n))= 0.2 exp(jwk) 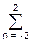 exp(-jwn).
exp(-jwn).
Отсюда, выражение для передаточной функции:
H(w) = 0.2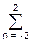 exp(-jwn) = 0.2[exp(2jw)+exp(jw)+1+exp(-jw)+exp(-2jw)],
exp(-jwn) = 0.2[exp(2jw)+exp(jw)+1+exp(-jw)+exp(-2jw)],
что полностью идентично выражению (10.1.2).
Следует запомнить: если оператор фильтра известен, то для получения его частотной характеристики достаточно подставить сигнал exp(jwn) непосредственно в линейное уравнение фильтра. Тем самым выполняются сразу 2 операции: производится z- преобразование h(n) и подставляется z = exp(-jwn), т.е. осуществляется трансформация h(n)→ h(z) → H(w).
Так как импульсная реакция фильтра МНК симметрична (функция h(n) четная), частотное представление передаточной функции должно быть вещественным, в чем нетрудно убедиться, объединив комплексно сопряженные члены выражения (10.1.2):
H(w) = 0.2(1+2 cos w+2 cos 2w).
Альтернативное представление передаточной функции H(w) для фильтра с произвольным количеством коэффициентов 2N+1 нам достаточно хорошо известно, как нормированный фурье-образ прямоугольной функции, каковой по существу и является селектирующее окно фильтра (10.1.1):
H(w) = sin((N+1/2)w)/[(N+1/2)w] = sinc((N+1/2)w). (10.1.3)
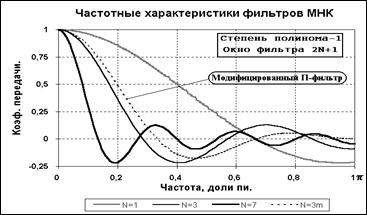
Рис. 10.1.2. Сглаживающие фильтры МНК.
Графики передаточных функций (10.1.3) приведены на рисунке 10.1.2. По графикам можно видеть коэффициент передачи сигнала с входа на выход фильтра на любой частоте. Без ослабления (с коэффициентом передачи 1) сглаживающим фильтром пропускается (и должен пропускаться по физическому смыслу сглаживания данных) только сигнал постоянного уровня (нулевой частоты). Этим же определяется и тот фактор (который стоит запомнить), что сумма коэффициентов сглаживающего НЦФ всегда должна быть равна 1 (отсчет ненормированного дискретного фурье-преобразования на частоте w = 0 равен сумме значений входной функции).
Чем больше число коэффициентов фильтра (шире окно фильтра), тем уже полоса пропускания низких частот. Подавление высоких частот довольно неравномерное, с осцилляциями передаточной функции отно- сительно нуля. На рис. 10.1.3 приведен пример фильтрации случайного сигнала (шума) фильтрами с различным размером окна.
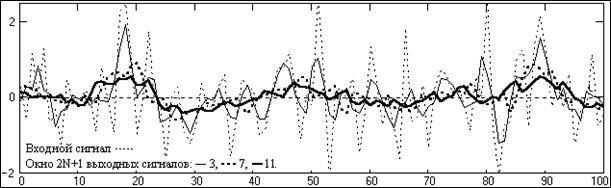
Рис. 10.1.3. Фильтрация шумов фильтрами МНК 1-го порядка.
Частотное представление передаточных функций позволяет наглядно видеть особенности фильтров и целенаправленно улучшать их харак- теристики. Так, если в рассмотренном нами фильтре с однородной импульсной реакцией hn = 1/(2N+1) уменьшить два крайних члена в 2 раза и заново нормировать к сумме S hn = 1, то частотные характеристики фильтра заметно улучшаются. Для нахождения передаточной функции моди- фицированного фильтра снимем в выражении (10.1.3) нормировку (умножим на 2N+1), вычтем значение 1/2 крайних членов (exp(-jwN)+exp(jwN))/2 = cos(wN) и заново пронормируем полученное выражение (разделим на 2N). Пример новой передаточной функции при N=3 также приведен на рисунке 10.1.2. Передаточные функции модифицированных таким образом фильтров приводятся к нулю на частоте Найквиста, при этом несколько расширяется полоса пропускания низких частот и уменьшается амплитуда осцилляций в области подавления высоких частот. Если смотреть на сглаживание, как на операцию подавления высокочастотных помех, то модифицированные фильтры без сомнения больше соответствует своему целевому назначению.
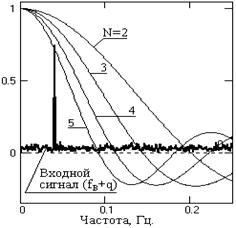 Рис. 10.1.4. Рис. 10.1.4. |
При выборе окна фильтра следует учитывать как коэффициент подавления дисперсии шумов, так и степень искажения полезного сигнала, на который наложены шумы. Оптимальное окно фильтра может быть определено только в том случае, если спектр сигнала известен и ограничен определенной верхней частотой, а мощность шумов не превы- шает определенного уровня. Рассмотрим это на конкретном примере.
Допустим, что нужно обеспечить максимальное подавление дисперсии шумов при минимальном искажении верхней граничной частоты сигнала fв, на которой мощность шумов равна мощности сигнальной гармоники fв. Значение fв равно 0.08 частоты Найквиста дискретизации данных, т.е. fв = 0.04 при Dt=1. Относительные значения мощности (дисперсии) гармоники и шума принимаем равными 1. Спектр модели сигнала + шума в сопоставлении с передаточными функциями фильтров приведен на рис. 10.1.4.
Таблица 10.1.1.
| N | ||||||||
| Ку(fв) | 0.98 | 0.94 | 0.88 | 0.8 | 0.7 | 0.6 | 0.51 | |
| Wu(N) | 0.96 | 0.88 | 0.77 | 0.64 | 0.51 | 0.38 | 0.26 | |
| Wq(N) | 0.33 | 0.2 | 0.14 | 0.11 | 0.09 | 0.08 | 0.07 | |
| Кс/ш(N) | 2.88 | 4.4 | 5.4 | 5.8 | 5.6 | 4.89 | 3.85 | |
| d2(N) | 0.35 | 0.23 | 0.18 | 0.17 | 0.18 | 0.21 | 0.26 | |
| s2(N) | 0.32 | 0.2 | 0.15 | 0.15 | 0.18 | 0.23 | 0.31 |
По формуле (10.1.3) вычисляем коэффициенты Ку(fв) усиления фильтров с N от 0 до 6 на частоте fв (см. таблицу 10.1.1). При мощности гармоники Wu = 1 амплитудное значение гармоники на входе фильтра равно U = 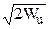 = 1.41. Мощности гармоник на выходе фильтров в зависимости от N:
= 1.41. Мощности гармоник на выходе фильтров в зависимости от N:
Wu(N)= 0.5·[U· Ку(fв)]2.
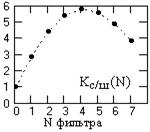 Рис. 10.1.5. Рис. 10.1.5. |
Соответственно, при мощности входного шума Wq=1 мощности шумов на выходе фильтров будут численно равны коэффициентам усиления дисперсии шумов Wq(N) = Wq·Kq(N).
Максимум отношения
Кс/ш(N) = Wq(N)/Wu(N)
определяет оптимальный фильтр с максимальным увеличением отношения сигнал/шум, т.е., по существу, коэффициент усиления отношения сигнал/шум при выполнении фильтрации с учетом изменения амплитудных значений полезной части сигнала.
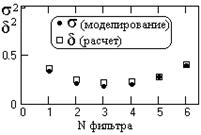 Рис. 10.1.6. Рис. 10.1.6. |
При Ку(fв) > 0.5 и Wu(N) = Wq(N) = 1 численные значения величины d2(N) = 1/ Кс/ш(N) в первом приближении могут служить оценкой s2(N) квадрата среднего квадратического отклонения выходных сигналов от "чистой" гармоники fв, заданной на входе. Свидетельством этому служат последние строки таблицы 10.1.1, где приведены результаты математического моделирования фильтрации по данным условиям на выборке 10000 точек. На рис. 10.1.6 приведены результаты сопоставления расчетных d2(N) и модельных s2(N) значений данных коэффициентов. Эффект фильтрации можно видеть на рис. 10.1.7, где приведен пример сигналов моделирования на ограниченном отрезке данных.
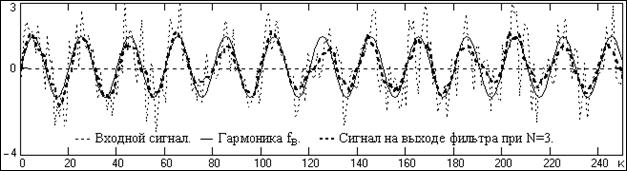
Рис. 10.1.7. Сигналы на входе и выходе фильтра МНК 1-го порядка.
 2014-02-13
2014-02-13 1942
1942








