Рассмотрим теперь pn -переход, к которому приложено прямое смещение Vсм (минус батареи к n -типу, плюс – к p -типу). Для того чтобы описать вольт-амперные характеристики (ВАХ) pn -перехода допустим, что все приложенное внешнее напряжение падает на pn- переходе.
При прямом смещении высота потенциального барьера понижается на qVсм по сравнению с равновесным состоянием, соответственно изменяется и толщина ОПЗ:
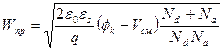 . . | (5.17) |
Понижение потенциального барьера приводит к увеличению потока основных носителей заряда по сравнению с равновесным состоянием. Под действием диффузионных процессов основные носители (nn и pp) перемещаются в соседнюю область, становясь неосновными носителями (pn и np). Образовавшийся градиент концентрации неосновных носителей приводит к появлению диффузионных токов неосновных носителей заряда, он направлен от ОПЗ вглубь полупроводника (рис. 5.4). При этом направления диффузионных токов, создаваемых pn и np совпадают, в то время как их потоки направлены в разные стороны.
Ограничимся пока рассмотрением n -области pn -перехода. В n -области появившиеся неосновные носители (дырки) с концентрацией 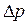 (рис. 5.4, а) создают в первый момент вблизи контакта положительный объемный заряд, однако через максвелловское время релаксации будет скомпенсирован объемным зарядом основные носителей заряда – электронов, которые под действием электрического поля, созданного избыточными дырками, будут подтянуты в количестве
(рис. 5.4, а) создают в первый момент вблизи контакта положительный объемный заряд, однако через максвелловское время релаксации будет скомпенсирован объемным зарядом основные носителей заряда – электронов, которые под действием электрического поля, созданного избыточными дырками, будут подтянуты в количестве 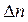 из глубины n -области, а в n -область электроны поступит из внешней цепи. Электроны будут двигаться за счет поля, создаваемого избыточными дырками и по свой природе является дрейфовым.
из глубины n -области, а в n -область электроны поступит из внешней цепи. Электроны будут двигаться за счет поля, создаваемого избыточными дырками и по свой природе является дрейфовым.
В состоянии термодинамического равновесия дрейфовый ток основных носителей должен компенсировать диффузионный ток неосновных носителей и суммарный ток через pn -переход равен нулю.
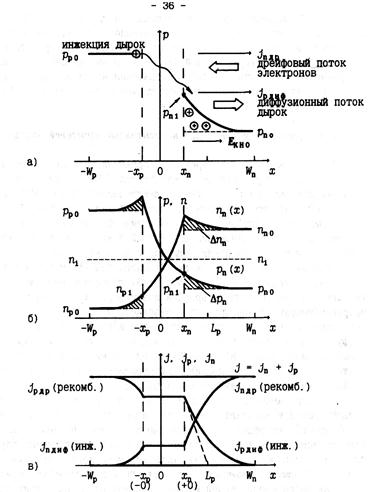 |
| Рис. 5.4 |
Во всех частях электронного полупроводника будет соблюдаться электронейтральность, но в приконтактной области pn -перехода концентрация электронов и дырок будет повышена на 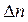 =
=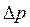 по сравнению с равновесным состоянием. Введение в полупроводник носителей заряда с помощью pn -перехода при подаче на него прямого смещения в область, где это носители заряда являются неосновными, называют инжекцией. Теперь концентрация дырок в n -области вблизи контакта будет равна:
по сравнению с равновесным состоянием. Введение в полупроводник носителей заряда с помощью pn -перехода при подаче на него прямого смещения в область, где это носители заряда являются неосновными, называют инжекцией. Теперь концентрация дырок в n -области вблизи контакта будет равна:
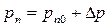 . . | (5.18) |
Для ее нахождения в стационарном случае на границе с ОПЗ (при x=Wn) нужно в (5.5) место qφк использовать значение q(φк-Vсм).
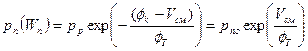 , , | (5.19) |
Таким образом, концентрация неосновных носителей в низколегированной области (базе) зависит от концентрации носителей в высоколегированной области (эмиттере) и от напряжения смещения, приложенного к pn-переходу (рис.5.5).
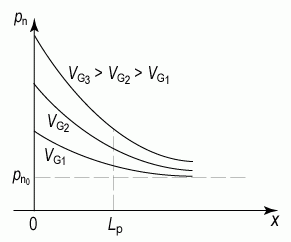 |
| Рис. 5.5 |
Из (5.19) следует, что концентрация избыточных носителей в n -области при x=Wn равна:
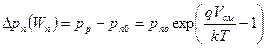 . . | (5.20) |
Аналогичные явления происходят в p -области: сюда из n - области инжектируются электроны и концентрация избыточных электронов при x=-Wp составит:
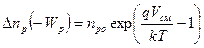 . . | (5.21) |
Если к pn -переходу приложено обратное смещение (минус батареи к p -типу, плюс – к n -типу) (рис. 5.5, б), потенциальный барьер повышается на qVсм. Толщина слоя ОПЗ увеличивается:
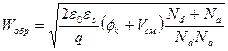 . . | (5.22) |
Чем сильнее переход смещен в обратном направлении, тем выше потенциальный барьер, и тем меньшее количество основных носителей заряда способно преодолеть возросший потенциальный барьер. В соответствии с этим количество неосновных носителей заряда в приконтактной области уменьшается по сравнению с равновесным состоянием, следовательно, уменьшается и количество основных носителей заряда вследствие соблюдения электронейтральности. Это явление носит название экстракции носителей заряда.
Таким образом, при обратном смещении pn -перехода ток основных носителей заряда будет меньше, чем при равновесном состоянии, а ток неосновных носителей заряда практически не изменится. Поэтому суммарный ток через pn -переход будет направлен от n -области к p -области и с увеличением обратного напряжения вначале будет незначительно расти, а затем стремиться к некоторой величине, называемой током насыщения Js.
Для аналитического расчета ВАХ pn -перехода примем следующие допущения:
1. Модель электронно-дырочного перехода одномерная; p - и n -области имеют бесконечную протяженность.
2. Переход тонкий, носители заряда пролетают через ОПЗ без рекомбинации (ОПЗ стянут в линию).
3. Обе квазинейтральные области сильно легированы, падением напряжения на них можно пренебречь. Вся внешняя разность потенциалов приложена к pn -переходу.
4. Рекомбинацию считаем линейной.
5. Уровень инжекции мал (Δ np<<pp 0, Δ p<< nn 0).
Чтобы рассчитать ВАХ pn -перехода, нужно найти закон изменения концентрации свободных носителей заряда в p - и n - областях. Для этого необходимо решить уравнения непрерывности:
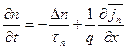 | (5.23) |
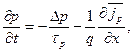 | (5.24) |
Для любых полей плотность полного тока дырок и электронов, определяющаяся дрейфовыми и диффузионными составляющими, будет равна:
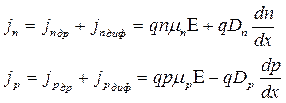 | (5.25) |
где 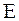 - напряженность внешнего электрического поля.
- напряженность внешнего электрического поля.
Общий ток через образец должен оставаться постоянным: 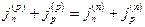 .
.
Рассмотрим n -область. При нахождении статической ВАХ концентрация носителей не меняется во времени. В стационарном состоянии
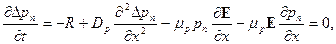 | (5.26) |
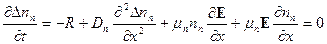 | (5.27) |
Эти уравнения справедливы без учета встречных потоков электронов и дырок, но возрастание концентрации носителей увеличивает вероятность их рассеяния! Для учета этих процессов, проведем следующие операции: учитывая квазинейтральность области Δ nn= Δ pn, и соотношение Эйнштейна (3.24), умножая уравнение (5.26) на 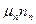 и уравнение (5.27) на
и уравнение (5.27) на 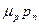 , для стационарного случая получим:
, для стационарного случая получим:
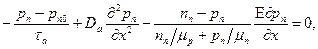 | (5.28) |
где 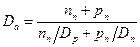 - коэффициент амбиполярной диффузии,
- коэффициент амбиполярной диффузии, 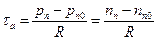 - амбиполярное время жизни.
- амбиполярное время жизни.
В случае малого уровня инжекции (т.е. при 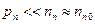 в полупроводнике n -типа) уравнение (5.25) упрощается:
в полупроводнике n -типа) уравнение (5.25) упрощается:
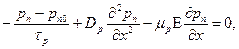 | (5.29) |
Но в квазинейтральной области напряженность внешнего электрического поля равна нулю! Таким образом, плотность тока в n -области определяется диффузионным током дырок, зависящим от их градиента концентрации.
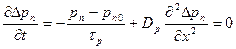 | (5.30) |
Используя соотношение 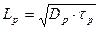 , получим:
, получим:
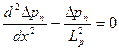 | (5.31) |
Общее решение такого уравнения имеет вид:
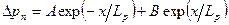 | (5.32) |
Так как при движении избыточных носителей в объем полупроводника (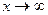 ) их концентрация спадает до нуля, постоянная B должна быть принятой равной нулю. Тогда из (5.16) получим:
) их концентрация спадает до нуля, постоянная B должна быть принятой равной нулю. Тогда из (5.16) получим:
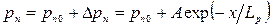 . . | (5.33) |
Концентрация неравновесных дырок на границе ОПЗ при x=Wn, согласно (5.19) равна:
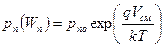 , , | (5.34) |
учитывая это, находим при x=Wn:
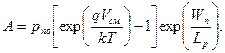 | (5.35) |
Окончательно закон изменения концентрации неравновесных дырок в n -области при x>Wn принимает вид:
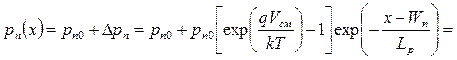 . . 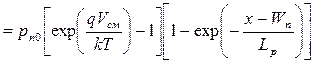 | (5.36) |
На основании (5.25) при 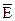 =0 получаем:
=0 получаем:
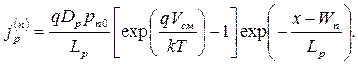 | (5.37) |
На границе ОПЗ при x=Wn, получим:
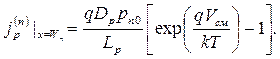 | (5.38) |
Проведем аналогичные рассуждения для p -области при x<-Wp и получим:
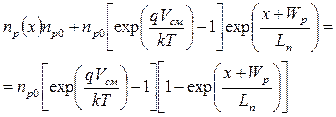 . . | (5.39) |
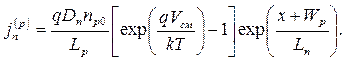 | (5.40) |
На границе ОПЗ при x=-Wp, получим:
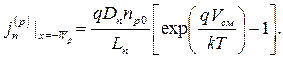 | (5.41) |
Следовательно, ВАХ тонкого pn -перехода описывается уравнением:
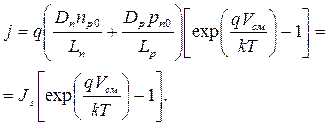 | (5.42) |
где плотность тока насыщения
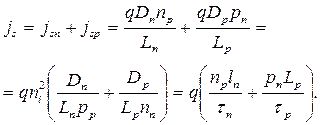 | (5.43) |
Формулу (5.42) часто называют формулой Шокли.
Таким образом, при прямом смещении ток, текущий через pn -переход, экспоненциально возрастает, а обратный ток растет медленно и достигает тока насыщения. Выпрямляющие свойства pn -перехода тем лучше, чем меньше ток насыщения. Плотность тока насыщения уменьшается с ростом концентрации основных носителей заряда (т.е. с увеличением степени легирования областей). Причем, изменяя степень легирования областей, мы можем задавать условия для преимущественного протекания через барьер электронных или дырочных потоков. Именно эти свойства избирательного управления потоками носителей заряда легли в основу большей части биполярных приборов.
Кривые распределения концентрации равновесных и избыточных носителей заряда и токов через pn -переход для прямого и обратного смещений изображены на рис. 5.6.
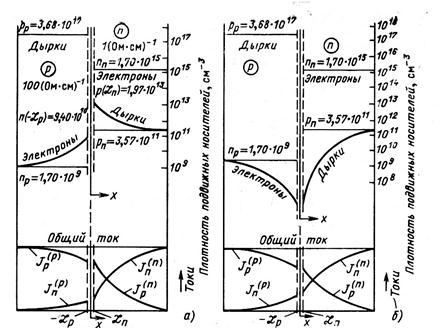 |
| Рис. 5.6. Концентрации носителей заряда и токи в p-n-переходе при прямом (а) и обратном (б) смещении |
Токи неосновных носителей спадают до нуля от границы ОПЗ в глубь полупроводника, поскольку спадают градиенты концентраций носителей.
На границе ОПЗ (х=0) инжекционный ток дырок 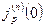 и инжекционный ток электронов
и инжекционный ток электронов 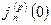 составляют полный ток через переход
составляют полный ток через переход 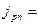
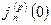 +
+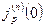 . Полный ток постоянен во всей структуре диода. Тогда рекомбинационные токи основных носителей получим вычитанием в каждом сечении структуры из полного тока ток неосновных носителей. Уменьшение тока основных носителей, полученное нами формально, имеет физическое обоснование. В силу электронейтральности распределение приращений концентрации основных носителей повторяет распределение приращения неосновных носителей. Диффузионные составляющие токов основных носителей в каждой области вычитаются из дрейфовых токов в этих областях, поскольку направления дрейфового и диффузионного тока противоположны. При обратных смещениях (
. Полный ток постоянен во всей структуре диода. Тогда рекомбинационные токи основных носителей получим вычитанием в каждом сечении структуры из полного тока ток неосновных носителей. Уменьшение тока основных носителей, полученное нами формально, имеет физическое обоснование. В силу электронейтральности распределение приращений концентрации основных носителей повторяет распределение приращения неосновных носителей. Диффузионные составляющие токов основных носителей в каждой области вычитаются из дрейфовых токов в этих областях, поскольку направления дрейфового и диффузионного тока противоположны. При обратных смещениях (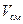 <0) токи выражаются в соответствии с (5.37) и (5.40) формулами:
<0) токи выражаются в соответствии с (5.37) и (5.40) формулами:
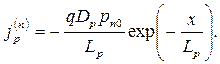 | (5.44) |
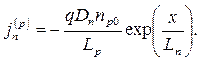 | (5.45) |
Абсолютное значение полного обратного тока
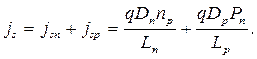 | (5.46) |
Рассмотрим Si pn -переход. 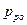 = Na =1018 cм-3,
= Na =1018 cм-3,
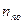 = Nd =1015 cм-3, в этом случае
= Nd =1015 cм-3, в этом случае
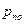 = 105 cм-3,
= 105 cм-3, 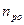 =102 cм-3
=102 cм-3
При прямом смещении:
Пусть 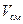 =0,6 В,
=0,6 В, 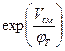 =
=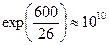
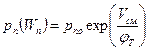 =1015 cм-3 равна
=1015 cм-3 равна 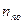
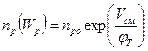 =1012 cм-3
=1012 cм-3
При обратном смещении:
Уже при 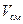 =-3
=-3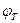 =-78 мВ,
=-78 мВ, 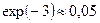 , т.е. граничные концентрации составляют 5% от исходных
, т.е. граничные концентрации составляют 5% от исходных 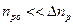 и
и 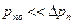 .
.
Распределение концентраций неосновных носителей описываются соотношениями:
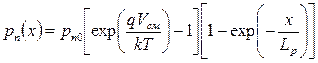
Толщиной ОПЗ пренебрегли, исходя из 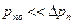 .
.
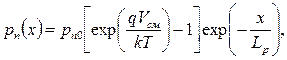
Аналогично для электронов в p-области:
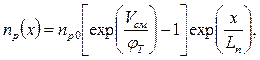
Знак показателя экспоненты для 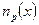 определяется выбором «0» на оси х.
определяется выбором «0» на оси х.
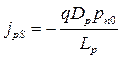 ,
, 
Параметры D и L зависят от концентраций примеси в областях. Для наших прикидок реальными будут: 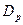 =2,5 см2/с,
=2,5 см2/с, 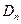 =25 см2/с,
=25 см2/с, 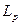 =14∙10-4 см,
=14∙10-4 см, 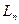 =20∙10-4 см. Тогда
=20∙10-4 см. Тогда 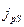 =0,3∙10-10 А/см2,
=0,3∙10-10 А/см2, 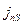 =2∙10-13 А/см2. Разница определяется главным образом отличием исходных значений
=2∙10-13 А/см2. Разница определяется главным образом отличием исходных значений 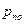 = 105 cм-3,
= 105 cм-3, 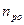 =102 cм-3.
=102 cм-3.
Оценим состав токов через pn -переход. Для прямого смещения, учитывая значения экспоненциального сомножителя 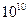 , получим:
, получим:
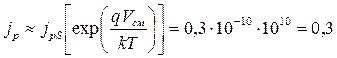 А/см2,
А/см2,
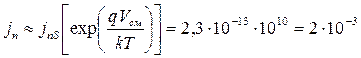 А/см2.
А/см2.
Ток через pn -переход является практически дырочным в следствие сильного легирования p- области и слабого легирования n- области.
Оценим, насколько справедливо в нашем примере предположение, что напряжение смещения приложено только к pn -переходу. Для полученного полного тока определим падение напряжения на толще n - и p -областей, приняв длину n -области 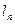 =0,01 см, длину p -области 1 мкм=10-4 см. Проводимости σn = qμnn, σp = qμpp. Подвижности μn и μp зависят от концентраций примеси в полупроводниках, исходя из данных, приведенных в литературе (Зи, Т.1, с. 34). μn = 300 см2/В∙с, μp = 100 см2/В∙с.
=0,01 см, длину p -области 1 мкм=10-4 см. Проводимости σn = qμnn, σp = qμpp. Подвижности μn и μp зависят от концентраций примеси в полупроводниках, исходя из данных, приведенных в литературе (Зи, Т.1, с. 34). μn = 300 см2/В∙с, μp = 100 см2/В∙с.
σn = qμnn=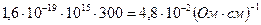
σp = qμpp=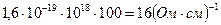
Падение напряжения на n - и p -слоях
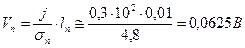

Таким образом, 10% от напряжения падает на слаболегированной области.
Изменение концентрации носителей в приконтактной области должно повлечь за собой изменение положения уровня Ферми. При приложении к pn -переходу внешнего напряжения состояние полупроводника становится неравновесным и характеризуется квазиуровнями Ферми Fn и Fp. Избыточные носители существуют в приконтактной области справа и слева от pn -перехода на расстоянии нескольких диффузионных длин и в этих областях квазиуровнями Ферми будут зависеть от координаты x (рис. 5.7).
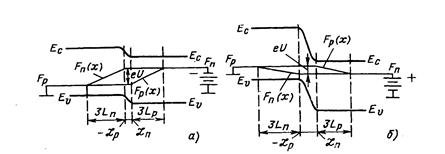 |
| Рис. 5.7. Энергетические диаграммы при прямом и обратном смещении |
Повышение температуры приводит к росту собственной концентрации, а следовательно, и к росту тока насыщения (рис. 5.8), поэтому стремятся использовать полупроводниковые материалы с большей запрещенной зоной (Si, GaAs, SiC).
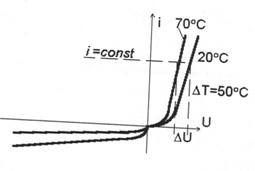 |
| Рис. 5.8. Изменение ВАХ при повышении температуры |
 2014-02-13
2014-02-13 4124
4124







