Задачи, решаемые при разработке логических схем цифровых устройств можно разделить на две категории:
- синтеза,
- анализа.
Синтез – это процесс построения устройства по заданному описанию с использованием того или иного математического аппарата.
Анализ задача обратная синтезу.
Модель цифрового устройства, отражающая его свойства по переработке сигналов, называется цифровым или дискретным автоматом. Существуют комбинационные цифровые автоматы, у которых выходные сигналы зависят лишь от текущего набора входных сигналов и последовательностные цифровые автоматы (автоматы с памятью) у которых набор выходных сигналов зависит не только от входного набора, но и от предшествующего по времени внутреннего состояния автомата и набора выходных сигналов.
В общем случае, модель цифрового автомата (рис.2) представляет собой многополюсный черный ящик с n входами и m выходами. Состояние автомата определяется состояниями сигналов на его входах и выходах. Совокупность входных и выходных переменных Х и Y образуют входное и выходное слово автомата, соответственно.

Рис.3.1 Схема представления цифрового автомата в виде многополюсника
Различные значения входных переменных образуют алфавит (т.к. алфавит входных и выходных переменных един, в дальнейшем будет рассматриваться только один алфавит). В цифровой технике алфавит входного (выходного) слова содержит два значения (две буквы) "1" и "0". Каждое слово - набор переменных на входе или на выходе автомата, отличается от другого слова хотя бы одной буквой. Каждая буква слова поставлена в соответствие с номером входа (выхода). Зависимость выходных переменных Y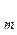 ,…,Y
,…,Y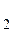 , Y
, Y выраженная через совокупность входных переменных X
выраженная через совокупность входных переменных X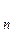 ,…,X
,…,X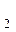 ,X
,X с помощью алгебры логики, носит название функции алгебры логики. Для n-разрядного двоичного кода X
с помощью алгебры логики, носит название функции алгебры логики. Для n-разрядного двоичного кода X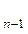 ,…, X
,…, X , X
, X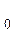 существует 2
существует 2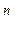 различных значений Y
различных значений Y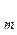 . Функция называется полностью определенной, если заданы все 2
. Функция называется полностью определенной, если заданы все 2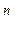 ее значений. Если часть значений функции не задана, она называется частично определенной.
ее значений. Если часть значений функции не задана, она называется частично определенной.
Для описания логических функций используются различные способы:
1. Словесное описание наиболее часто применяется для первичного описания поведения устройства. Например, Y=1, если X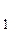
 X
X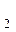 и Y=0, если X
и Y=0, если X = X
= X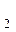 (такая логическая функция носит название схемы неравнозначности).
(такая логическая функция носит название схемы неравнозначности).
2. Табличное представление.
Например, для схемы неравнозначности:
Таблица 3.1
| N | X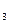 | X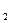 | X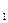 | Y |
Такая таблица называется таблицей истинности.
3. Описание логической функции в виде алгебраического выражения.
Формула для таблицы 3.1 будет выглядеть следующим образом:
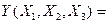
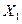 *
*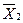 *
*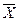
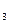 +
+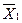 *
*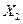 *
*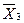 +
+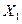 *
*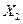 *
*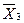 +
+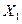 *
*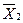 *
*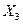 . (3.14)
. (3.14)
4. Описание в виде кодированной функции, когда функция представляется, например, в виде дизъюнкции конъюнкций, но конъюнкции записываются в виде десятичных чисел. Так (3.14) будет выглядеть следующим образом, при условии, что X 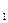 соответствует младшему разряду числа, а X
соответствует младшему разряду числа, а X 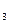 - старшему:
- старшему:
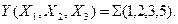
5. Описание в виде алгоритма, например на языке VHDL (Very hight speed integrated circuit Hardware Description Language):
Y<= ((X1 and not X2 and not X3) or (not X1 and X2 and not X3) or (X1 and X2 and not X3) or (X1 and not X2 and X3))
6. Графическое описание, при этом цифровое устройство представляется в
виде схемы электрической принципиальной, выполненной с использованием условных графических изображений. В частности для изображения элементов, выполняющих операции И, ИЛИ и НЕ (конъюнкцию, дизъюнкцию и отрицание), приняты следующие графические изображения:
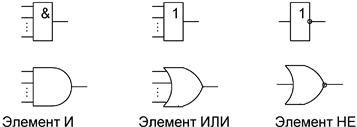
Рис. 3.2. Пример графических изображений логических элементов
Один из вариантов схемы, реализующей (14), приведен на рисунке 4:
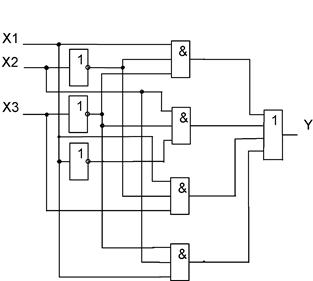
Рис. 3.3 Пример схемы, реализующей логическую функцию.
Алгебра логики позволяет создавать сложные функции, аргументы которых есть функции других двоичных аргументов. При этом возникает задача упрощения функций с целью обеспечения простоты схемной реализации. Операция замены аргумента одной функции другими, более простыми носит название суперпозиции функции. Многократное использование суперпозиции позволяет упрощать выражения для функций.
Элементарная конъюнкция представляет собой конъюнкцию конечного числа переменных и их инверсий, например:
Y(X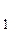 , X
, X 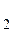 , Х
, Х 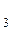 ) =
) = 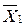 * X
* X  *
*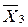 , (3.15)
, (3.15)
является элементарной конъюнкцией переменных X , X
, X , Х
, Х  .
.
Элементарная дизъюнкция представляет собой дизъюнкцию конечного числа переменных и их инверсий, например:
Y(X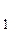 , X
, X 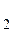 , Х
, Х 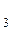 ) = X
) = X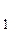 +X
+X 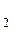 + Х
+ Х 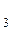 , (3.16)
, (3.16)
является элементарной дизъюнкцией переменных X , X
, X 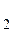 , Х
, Х 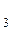 .
.
Количество переменных в элементарной конъюнкции (дизъюнкции) называется ее длиной и определяет ее ранг. Так выше приведены элементарные конъюнкции и дизъюнкции третьего ранга.
Минтермом называют функцию, которая принимает единичное значение при одном из всех возможных наборов аргументов, а макстермом называют функцию, которая принимает нулевое значение при одном из всех возможных наборов аргументов. Если число аргументов n, то число минтермов и макстермов N=2 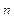 .
.
Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой ДНФ. Например: X 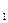 *
*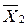 *
*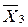 +
+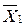 * X
* X 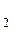 *
*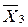 + X
+ X 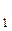 .
.
Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой КНФ. Например:
(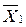 + X
+ X 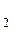 + Х
+ Х 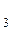 )*(X
)*(X 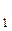 +
+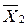 + Х
+ Х 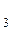 )*
)*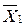 .
.
Нормальные формы логических функций принято называть каноническими. Любую логическую функцию можно, используя законы алгебры логики привести к каноническому виду. Для этого необходимо:
- избавиться от инверсий над выражениями, перейдя к форме, в которой есть инверсии только отдельных переменных;
- применяя закон дистрибутивности раскрыть скобки и привести конъюнкции (дизъюнкции) к элементарным.
Если в состав логической формулы входят наборы одинакового ранга, связанные конъюнкцией (дизъюнкцией), то такая форма представления логической функции носит название совершенной дизъюнктивной (конъюнктивной) нормальной формы СДНФ (СКНФ). Пример приведен в таблице 2.2.
Выражения, где определены минтермы носят название конституент единицы, а там, где определены макстермы - конституент нуля.
Искомая логическая функция СДНФ (СКНФ) получается дизъюнкцией минтермов (конъюнкцией макстермов). СКНФ используется при синтезе реже.
Произведения, входящие в СДНФ носят название импликант. По определению, импликантой называется логическая функция 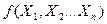 , входящая в
, входящая в 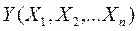 , если для любого набора
, если для любого набора 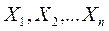 , при котором
, при котором 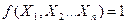 ,
, 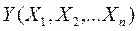 также равно единице.
также равно единице.
Импликанта называется простой, если она не может быть поглощена другими импликантами, входящими в данную функцию.
По полученным СДНФ (СКНФ) реализуются принципиальные логические схемы. СДНФ(СКНФ) не являются самыми простыми формами представления логических функций.
В общем случае переход от табличного представления к алгебраическому осуществляется по формуле:
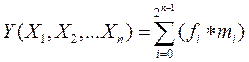 , (17)
, (17)
являющейся одной из основных в алгебре логики.
В (17) 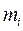 - минтермы переменных
- минтермы переменных 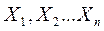 ,
, 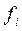 - принимает значение лог. «1», если для данного набора
- принимает значение лог. «1», если для данного набора 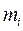 ,
, 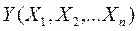 равна лог. «1» и
равна лог. «1» и 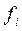 - принимает значение лог. «0», если для данного набора
- принимает значение лог. «0», если для данного набора 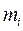 ,
, 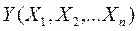 равна лог. «0».
равна лог. «0».
Существуют и другие методы задания и оптимизации логических функций, например, ранее при числе переменных не более шести применялся метод диаграмм Карно-Вейча. Карты Карно – это графическое представление таблиц истинности.
Таблица 3.2
X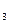 | X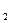 | X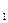 | Y | СДНФ | СКНФ |
| минтерм | макстерм | ||||
| - | X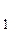 +X +X 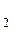 + Х + Х 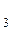 | ||||
X 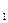 * *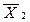 * *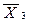 | - | ||||
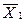 * X * X 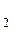 * *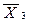 | - | ||||
| - | 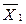 + +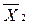 + Х + Х 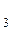 | ||||
| - | X +X +X 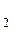 + +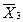 | ||||
X 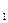 * *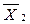 * Х * Х 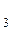 | - | ||||
| - | X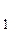 + + 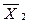 + +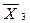 | ||||
| - | 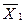 + X + X 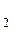 + +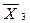 |
Каждой комбинации переменных в соответствие ставится одна клетка карты. Таким образом, число клеток в карте при числе переменных n равно 2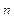 .
.
Правила построения карты Карно следующие:
1) Слева и сверху располагаются значения аргументов. Порядок размещения аргументов таков, что в двух соседних столбцах или строках отличается значение только одного аргумента. При этом соседними считаются столбцы и строки, находящиеся на противоположных краях таблицы.
2) В ячейки заносятся соответствующие значения логической функции.
3) Соседние единичные ячейки объединяются в прямоугольники по 2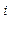 ячеек.
ячеек.
4) Для каждого прямоугольника записывают произведение тех аргументов, которые в соседних клетках не изменяют своего значения.
5) Переменные входят в произведения в прямом виде, если их значение в соседних клетках равно «1», в противном случае в инверсном.
6) От полученных значений образуется дизъюнкция.
Рассмотрим пример построения карты Карно для таблицы истинности 3.1.
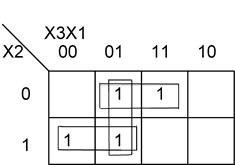
Рис. 3.5 Пример реализации карты Карно.
Имеется три прямоугольника:
1. X 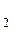 *
*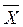
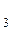 , здесь X
, здесь X 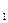 меняет свое значение,
меняет свое значение,
2. X 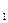 *
*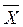
 , здесь X
, здесь X 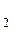 меняет свое значение,
меняет свое значение,
3. X 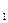 *
*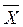
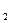 , здесь Х
, здесь Х 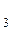 меняет свое значение,
меняет свое значение,
а логическая формула будет представлена следующим образом:
Y(X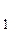 , X
, X 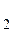 , Х
, Х 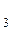 ) = X
) = X 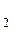 *
*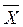
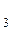 + X
+ X 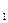 *
*
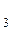 + X
+ X 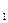 *
*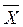
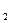 . (3.18)
. (3.18)
Как видно, получилась формула проще (3.14), хотя она реализует ту же функцию. Выражение (3.18) состоит из «не склеивающихся» конъюнкций переменных, т. е. простых импликант.
 2014-02-13
2014-02-13 2497
2497
