Речь идет о планировании эксперимента по идентификации модели более высокого порядка (квадратичной) вида:
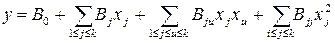 . (3.65)
. (3.65)
Число опытов должно быть не меньше, чем
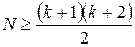 . (3.66)
. (3.66)
Кроме того, необходимо, чтобы каждый фактор варьировался не менее, чем на трех уровнях. Опыты могут проводиться в одной из двух областей: на k- мерном гиперкубе 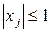 или на k- мерном гипершаре
или на k- мерном гипершаре 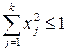 .
.
Расчет коэффициентов уравнения (3.65) также проводится МНК, что соответствует матричной форме записи
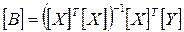 . (3.67)
. (3.67)
Для построения модели (3.65) предложено большое количество планов. Наиболее широко распространены так называемые симметричные планы: планы типа 3k , разного рода композиционные (ортогональные, ротатабельные, типа Вk); некомпозиционные планы Бокса-Бенкина; квази- D -оптимальные планы Песочинского и др.
В качестве примера рассмотрим композиционные планы. В данном случае композиционность означает последовательную достройку линейных планов до планов второго порядка. Эта процедура предполагает реализацию опытов ПФЭ или ДФЭ, а затем добавление к этим опытам («ядру» плана) некоторого количества, так называемых, «звездных точек». Такие планы обычно называют центральными, поскольку все опыты располагаются симметрично вокруг центра плана – основного уровня.
Например, один из центральных композиционных планов для k = 2 имеет вид
Таблица 3.5.
| Номер опыта | х1 | х2 | Примечание |
| 1-4 | 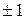 | 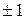 | ПФЭ – ядро плана |
| 5-8 | 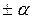 | 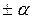 | «звездные точки» |
| основной уровень – центр плана |
Общее число опытов N композиционных планов при k факторах (если опыты не дублируются) равно
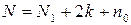 , (3.68)
, (3.68)
где 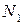 – число опытов в ядре плана (
– число опытов в ядре плана (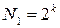 ,если ядро плана ПФЭ и
,если ядро плана ПФЭ и
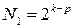 , если ядро плана ДФЭ);
, если ядро плана ДФЭ);
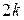 – число «звездных точек»;
– число «звездных точек»;
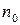 – число опытов в центре плана.
– число опытов в центре плана.
Последовательность решения задачи состоит в следующем. Вначале ставят опыты 1-4, составляющие ядро плана и позволяющие построить либо линейную модель вида
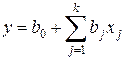 , (3.69)
, (3.69)
либо неполную квадратичную модель вида
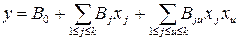 . (3.70)
. (3.70)
Если эти модели окажутся неадекватными, то добавляют опыты в звездных точках 5-8 и в центре плана (точка 9), что позволяет построить уже квадратичную модель.
| (3.79) |
Рассмотрим некоторые примеры решения технологических задач с применением планирования эксперимента, взятые из книги А.А. Спиридонова [12].
Пример 1 ИССЛЕДОВАНИЕ УПРУГОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ ШПИНДЕЛЬ — ДЕТАЛЬ ТОКАРНОГО СТАНКА
В Уральском техническом университете С. И. Солониным исследовано влияние факторов процесса резания на упругую характеристику системы шпиндель — деталь токарного станка. При точении деталей, консольно закрепленных в патроне, положение оси вращения в зоне обработки определяется положениями звеньев системы шпиндель — деталь. К этим звеньям относятся опоры шпинделя, шпиндель, патрон и деталь. В процессе точения система «шпиндель — деталь» упруго деформируется под действием силы резания. Если рассматривать обработку деталей большой жесткости, упругими деформациями которых можно пренебречь, то схема деформации системы под действием силы P, эквивалентной силе резания, будет иметь вид, изображенный на рис. 3.3.
Упругие деформации системы шпиндель — деталь будут определяться главным образом упругими деформациями стыков между шпинделем и опорами, шпинделя с патроном и стыка патрон — кулачки — деталь. Деформации стыков приводят к повороту звеньев друг относительно друга на углы 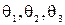 . В результате ось системы шпиндель — деталь получает форму ломаной линии, а ось системы в зоне обработки, будет повернутой и смещенной и располагается так, как это показано на рис. 3.3.
. В результате ось системы шпиндель — деталь получает форму ломаной линии, а ось системы в зоне обработки, будет повернутой и смещенной и располагается так, как это показано на рис. 3.3.
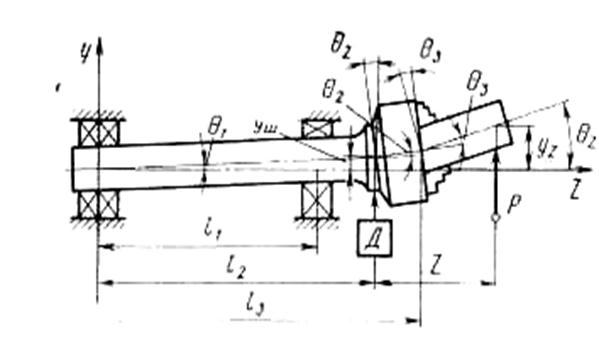
Рис. 3.3. Схема деформации системы шпиндель-деталь.
Для создания системы автоматического управления размером детали необходимо обеспечить измерение отклонений yz оси вращающейся детали в зоне обработки. Непосредственное измерение этих отклонений практически трудно осуществимо. Поэтому вместо уz измеряли упругое перемещение уш шпинделя в месте его соединения с патроном, а затем измеренную величину преобразовывали в оценку упругого перемещения оси шпинделя в зоне резания. В рассматриваемом случае указанное преобразование заключалось в  умножении перемещения уш оси шпинделя на упругую характеристику f(z) системы шпиндель — деталь. Измерение уш выполнялось с помощью индуктивного датчика Д. Упругая характеристика f(z) системы шпиндель — деталь представляет собой отношение уг к уш. Получена математическая модель, описывающая это отношение:
умножении перемещения уш оси шпинделя на упругую характеристику f(z) системы шпиндель — деталь. Измерение уш выполнялось с помощью индуктивного датчика Д. Упругая характеристика f(z) системы шпиндель — деталь представляет собой отношение уг к уш. Получена математическая модель, описывающая это отношение:

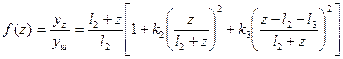 (3.83)
(3.83)
где z — координата, равная расстоянию от вершины резца до точки измерения yш; 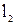 — расстояние от задней опоры шпинделя до стыка шпинделя с патроном;
— расстояние от задней опоры шпинделя до стыка шпинделя с патроном; 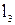 — расстояние от задней опоры шпинделя до стыка патрон – кулачки – деталь;
— расстояние от задней опоры шпинделя до стыка патрон – кулачки – деталь; 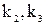 - коэффициенты, зависящие от упругих свойств стыков системы.
- коэффициенты, зависящие от упругих свойств стыков системы.
Величины упругих перемещений 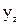 и
и 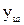 определяются величиной и направлением силы резания.
определяются величиной и направлением силы резания.
При выводе уравнения (3.83) сделано допущение о наличии прямой пропорциональной связи между силой нормального давления в стыке, деформацией стыка и углом 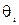 , его поворота. Так как силы нормального давления пропорциональны силе резания, то пропорциональны ей и упругие перемещения уz и уш. Имеются основания полагать, что при изменении силы P отношение уz/уш будет оставаться постоянным, т. е. величина и направление силы резания не будут оказывать существенного влияния на упругую характеристику
, его поворота. Так как силы нормального давления пропорциональны силе резания, то пропорциональны ей и упругие перемещения уz и уш. Имеются основания полагать, что при изменении силы P отношение уz/уш будет оставаться постоянным, т. е. величина и направление силы резания не будут оказывать существенного влияния на упругую характеристику 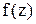 . Ее величина будет определяться только координатой z и упругими свойствами стыков, которые характеризуются коэффициентами k2 и k3. Для данного станка величины k2 и k3 можно считать постоянными.
. Ее величина будет определяться только координатой z и упругими свойствами стыков, которые характеризуются коэффициентами k2 и k3. Для данного станка величины k2 и k3 можно считать постоянными.
Изложенная физическая модель подвергалась экспериментальной проверке, которая производилась с помощью дробного факторного эксперимента и аппарата регрессионного анализа.
Были выбраны четыре фактора процесса резания, которые могли бы оказать влияние на величину упругой характеристики f(z):
t — глубина резания, мм;
s — подача, мм/об;
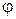 — главный угол в плане, град;
— главный угол в плане, град;
п — угловая скорость вращения детали, об/мин. Первые три фактора определяют величину и направление силы резания.
Для описания возможной связи упругой характеристики f(z) сфакторами t, s, 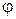 и п была принята простейшая математическая модель в виде полинома первой степени. Если обозначить f(z) в точке с фиксированным значением z через и, a t =
и п была принята простейшая математическая модель в виде полинома первой степени. Если обозначить f(z) в точке с фиксированным значением z через и, a t = 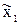 , s =
, s = 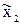 ,
, 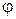 =
= 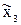 , n=
, n=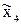 , то согласно принятой модели можно записать
, то согласно принятой модели можно записать
U=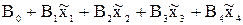 , (3.84)
, (3.84)
где Во, В1, В2, В3, В4 — коэффициенты полинома. Взаимодействиями факторов пренебрегаем. Если величина и не зависит от 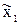 ,
, 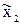 ,
, 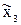 и
и 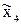 , то модель f(z) для фиксированного значения упругой характеристики z сведется к выражению u=
, то модель f(z) для фиксированного значения упругой характеристики z сведется к выражению u=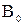 = const. Таким образом, задачей эксперимента было определение коэффициентов полинома, оценка значимости коэффициентов В1 В2, В3, В4 и проверка адекватности модели. Величина и характеризует функцию f(z) в точке с фиксированной величиной z, поэтому для оценки влияния t, s,
= const. Таким образом, задачей эксперимента было определение коэффициентов полинома, оценка значимости коэффициентов В1 В2, В3, В4 и проверка адекватности модели. Величина и характеризует функцию f(z) в точке с фиксированной величиной z, поэтому для оценки влияния t, s, 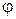 , n на f(z) были проведены исследования с различными значениями z. Величина z варьировалась от 200 до 320 мм с шагом 20 мм, при этом вылет детали из патрона соответственно изменялся от 40 до 160 мм.
, n на f(z) были проведены исследования с различными значениями z. Величина z варьировалась от 200 до 320 мм с шагом 20 мм, при этом вылет детали из патрона соответственно изменялся от 40 до 160 мм.
При проведении эксперимента каждый фактор варьировался на двух уровнях. Принятые в исследовании уровни факторов приведены в табл. 3.7
Для упрощения вычислений независимые переменные кодировались по выражению (3.7)
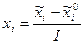 (3.85)
(3.85)
Коэффициенты полинома при кодированных переменных обозначим через 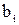 . Полином (3.84) после кодирования получил вид
. Полином (3.84) после кодирования получил вид
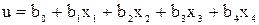 (3.44)
(3.44)
Уровни факторов Таблица 3.7
| Факторы | Интервалы варьирова- ния | Уровни факторов | ||
| верхний +1 | основной 0 | нижний —1 | ||
t, мм s, мм\об 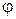 ,град n, об\мин ,град n, об\мин | 0,5 0,1 22,5 | 0,3 | 1,5 0,2 67,5 | 0,1 |
При выбранной модели использование дробного факторного эксперимента типа 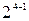 , предусматривающего проведение восьми опытов, позволяет получить эмпирические данные, необходимые для оценки коэффициентов уравнения регрессии и его статистического анализа. Матрица планирования в этом случае представляет собой полуреплику от плана эксперимента типа 24. В качестве генерирующего соотношения принято
, предусматривающего проведение восьми опытов, позволяет получить эмпирические данные, необходимые для оценки коэффициентов уравнения регрессии и его статистического анализа. Матрица планирования в этом случае представляет собой полуреплику от плана эксперимента типа 24. В качестве генерирующего соотношения принято 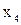 =
=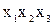 . Определяющий контраст равен
. Определяющий контраст равен 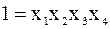 . Для оценки дисперсии воспроизводимости проводилось равномерное дублирование по два опыта в каждой точке факторного пространства
. Для оценки дисперсии воспроизводимости проводилось равномерное дублирование по два опыта в каждой точке факторного пространства
Матрица планирования и результаты опытов
Таблица 3.8
| Номер опыта | 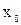 | 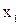 | 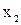 | 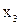 | 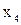 | 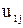 | 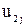 | 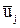 | 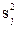 |
| + + + + + + + + | - + - + - + - + | - - + + - - + + | - - - - + + + + | - + + - + - - + | 3,75 4,64 4,95 4,83 4,25 4,38 4,00 4,52 | 4,39 4,15 4,44 4,55 3,94 4,94 4,64 4,94 | 3,97 4,40 4,70 4,69 4,10 4,66 4,32 4,73 | 0,2048 0,1201 0,1301 0,0392 0,0481 0,1568 0,2048 0,0882 | |
| Коэффи- циенты |  = =4,458 = =4,458 | 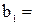 =0,161 =0,161 | 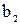 = =0,151 = =0,151 | 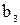 = =0,006 = =0,006 | 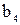 = =0,024 = =0,024 | 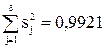 |
Матрица планирования и результаты опытов, выполненных при z=260 мм, указаны в табл. 3.8. Опыты выполнялись в случайной последовательности, Общее число опытов равно 16, а порядок их выполнения, установленный по таблице случайных чисел, следующий: 2, 15, 9, 5, 12, 14, 8, 13, 16, 1, 3, 7, 4, 6, 11, 10. Номера опытов выше 8-го относятся к повторным, например, условия опытов 1-го и 9-го одинаковы и соответствуют условиям 1-го опыта в матрице планирования и т. д. Для каждой серии опытов вычисляли среднее арифметическое 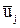 и дисперсию воспроизводимости опыта
и дисперсию воспроизводимости опыта 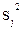 . Эту дисперсию определяли по выражению
. Эту дисперсию определяли по выражению
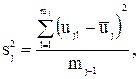 (3.87)
(3.87)
где l — номер опыта в j- йсерии; 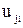 — значение функции отклика в l -м опыте j -й серии;
— значение функции отклика в l -м опыте j -й серии; 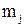 — число опытов в j -й серии.
— число опытов в j -й серии.
Вычисленные средние 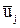 и дисперсии
и дисперсии 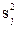 приведены в плане эксперимента таблице 3.8. Так как число
приведены в плане эксперимента таблице 3.8. Так как число 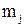 параллельных опытов в каждой серии одинаково, то однородность ряда дисперсий
параллельных опытов в каждой серии одинаково, то однородность ряда дисперсий 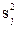 проверяли по G-критерию Кохрена:
проверяли по G-критерию Кохрена:
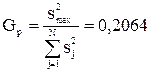 (3.88)
(3.88)
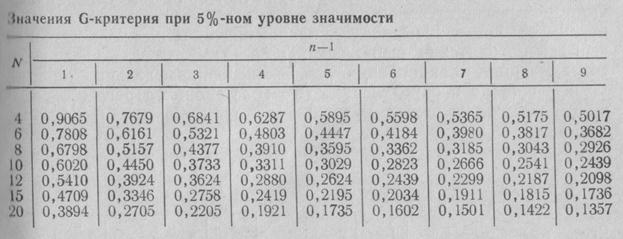
Табличное значение критерия при 5%-ном уровне значимости для N = 8 и т=2 GT=0,6798. Так как расчетное значение Gp = 0,2064 меньше табличного GT = 0,6798, гипотеза однородности дисперсий принимается. Убедившись в однородности дисперсий 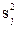 можно вычислить дисперсию s2 воспроизводимости эксперимента:
можно вычислить дисперсию s2 воспроизводимости эксперимента:
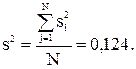 (3.89)
(3.89)
Коэффициенты 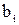 вычисляли по формуле (3.90)
вычисляли по формуле (3.90)
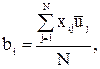 (3.90)
(3.90)
где 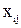 — кодированное значение i -го фактора в j -м опыте.
— кодированное значение i -го фактора в j -м опыте.
Вычисленные значения коэффициентов указаны в табл. 3.8 После подстановки в уравнение (3.86) значений коэффициентов 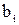 оно получило вид
оно получило вид
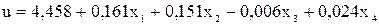 (3.91)
(3.91)
Для проверки гипотезы адекватности уравнения (3.91) находится дисперсия 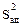 адекватности по формуле
адекватности по формуле
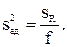 (3.92)
(3.92)
Остаточная сумма квадратов 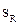 определена по выражению
определена по выражению
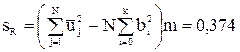 (3.93)
(3.93)
где: k — число исследуемых факторов; т = 2 - число параллельных опытов
f = N-(k+1)=3 - число степеней свободы.
Дисперсия адекватности составила 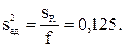
Гипотезу адекватности проверялась по F-критерию Фишера
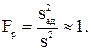
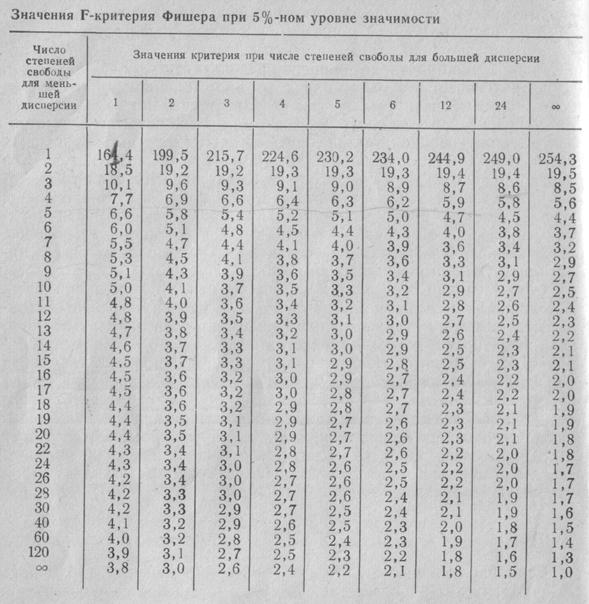
Табличное значение критерия Фишера при 5%-ном уровне значимости и числах степеней свободы для числителя 3 и знаменателя 8 равно 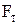 = 4,07. Так как FP<FT, модель, представленную уравнением (3.91) можно признать адекватной.
= 4,07. Так как FP<FT, модель, представленную уравнением (3.91) можно признать адекватной.
Для оценки значимости коэффициентов 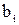 найдены их дисперсии
найдены их дисперсии
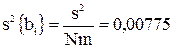
и определён доверительный интервал 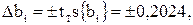
где tT = 2,3 — табличное значение критерия Стьюдента при 5% уровне значимости и числе степеней свободы N{m —1) =8.
Все коэффициенты, кроме  , меньше доверительного интервала, поэтому их можно признать статистически незначимыми и исключить из уравнения регрессии (3.91), которое в этом случае примет вид
, меньше доверительного интервала, поэтому их можно признать статистически незначимыми и исключить из уравнения регрессии (3.91), которое в этом случае примет вид
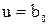 или u = 4,458.
или u = 4,458.
Для проверки возможности предсказания значений и по модели 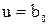 была вычислена дисперсия sp2 рассеяния результатов
была вычислена дисперсия sp2 рассеяния результатов 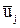 относительно их среднего, которым в данном случае является коэффициент
относительно их среднего, которым в данном случае является коэффициент  . Дисперсия sp2 определена по выражению
. Дисперсия sp2 определена по выражению
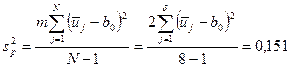
Однородность дисперсий sp2 и s2 проверена по F-критерию Фишера:
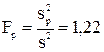
Табличное значение критерия Фишера при 5%-ном уровне значимости и числах степеней свободы для числителя 7 и для знаменателя 8 (табл.) FT = 3,50; расчётное значение критерия меньше табличного FP<FT, поэтому дисперсии sp2 и 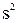 следует признать однородными, а полученную модель
следует признать однородными, а полученную модель 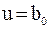 — адекватной.
— адекватной.
Адекватность модели 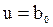 свидетельствует о несущественном влиянии глубины резания t, подачи s, угла в плане
свидетельствует о несущественном влиянии глубины резания t, подачи s, угла в плане 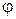 и числа оборотов n на величину упругой характеристики системы «шпиндель-деталь» f(z ), т. е. в области эксперимента при фиксированном значении осевой координаты z упругая характеристика f(z) остается постоянной при изменении t, s,
и числа оборотов n на величину упругой характеристики системы «шпиндель-деталь» f(z ), т. е. в области эксперимента при фиксированном значении осевой координаты z упругая характеристика f(z) остается постоянной при изменении t, s, 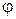 и п.
и п.
Аналогичные исследования были проведены при всех других принятых значениях z, а именно: z=200; 220; 240; 260; 280; 300; 320 мм. Математическая обработка экспериментальных данных показала, что в области эксперимента при принятых значениях z факторы t, s, 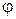 и п также не оказывают существенного влияния на величину упругой характеристики f(z).
и п также не оказывают существенного влияния на величину упругой характеристики f(z).
Опытные данные, 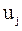 полученные при различных значениях z, позволили определить коэффициенты k2 и k3, характеризующие упругие свойства стыков системы. Эти коэффициенты, входящие в уравнение (3.83) упругой характеристики f(z), находились с использованием метода наименьших квадратов.
полученные при различных значениях z, позволили определить коэффициенты k2 и k3, характеризующие упругие свойства стыков системы. Эти коэффициенты, входящие в уравнение (3.83) упругой характеристики f(z), находились с использованием метода наименьших квадратов.
Проведенные исследования позволили получить упругую характеристику f(z) системы шпиндель — деталь токарного станка мод. 1К62, а также использовать предлагаемую методику для других станков токарной группы.
Использование полученной характеристики даёт возможность создать эффективную систему автоматического управления размером детали, обеспечивающую обработку с точностью до 3 класса.
Кроме того: линейная модель нулевого порядка это отсутствие функциональной зависимости, но отрицательный результат – в науке тоже результат!
Пример 2. ПОЛУЧЕНИЕ МОДЕЛИ, ХАРАКТЕРИЗУЮЩЕЙ ЗАВИСИМОСТЬ ТЕМПЕРАТУРЫ РЕЗАНИЯ ОТ ОСНОВНЫХ ФАКТОРОВ ПРОЦЕССА РЕЗАНИЯ
Рассмотрим методику получения зависимости температуры резания θ от скорости υ, подачи s и глубины резания t при обработке точением материала «сталь 20» цельными проходными резцами из быстрорежущей стали Р18.
Эмпирические температурные зависимости принято представлять степенными уравнениями регрессии вида
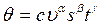 . (3.93)
. (3.93)
Для экспериментального получения степенных зависимостей их удобно логарифмировать с целью последующего использования мтода наименьших квадратов и последующим потенцированием.
Уравнение (3.47) после логарифмирования получит вид
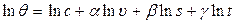 . (3.94)
. (3.94)
Для представления результатов эксперимента предлагается выбрать полиномом второй степени:
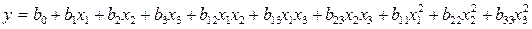 (3.95)
(3.95)
Где; 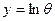 ;
;
θ – температура резания, записанная через аналого-цифровой преобразователь на компьютер;
x1, x2, x3 – кодированные (безразмерные) значения параметров v, s, t.
В качестве плана эксперимента использован центральный композиционный ротабельный план второго порядка. Кодирование независимых переменных производили с помощью соотношения [12]. Принятые в исследовании уровни факторов указаны в табл. 3.9.
Таблица 3.9
| Уровни факторов | Скорость резания. | Подача | Глубина резания | |||
| v, м/с | x1 | s, мм/об | x2 | t, мм | x3 | |
| Верхнее “звездное плечо”: | 0,725 | 1,682 | 0,463 | 1,682 | 1,49 | 1,682 |
| верхний | 0,454 | 0,26 | 1,04 | |||
| основной | 0,229 | 0,17 | 0,61 | |||
| нижний | 0,115 | -1 | 0,11 | -1 | 0,36 | -1 |
| Нижнее “звездное плечо”: | 0,072 | -1,682 | 0,082 | -1,682 | 0,25 | -1,682 |
Формулы преобразования натурных значений факторов в кодированные в данном случае имеют вид
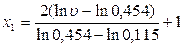 ;
; 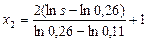 ;
;
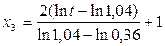 . (3.95)
. (3.95)
Матрица планирования и результаты опытов представлены в табл. 3.10
Матрица планирования и результаты опытов Таблица 3.10
| Номер опыта | x0 | x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | 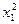 | 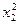 | 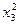 | y |
| + + + + + + + + | - + - + - + - + | - - + + - - + + | - - - - + + + + | + - - + + - - + | + - + - - + - + | + + - - - - + + | + + + + + + + + | + + + + + + + + | + + + + + + + + | 1,6879 2,0777 1,8499 2,2837 1,7787 2,1677 1,9479 2,3801 | |
| + + + + + + | -1,682 +1,682 | -1,682 +1,682 | -1,682 +1,682 | 2,829 2,829 | 2,829 2,829 | 2,829 2,829 | 1,6391 2,3311 1,8868 2,2016 1,9652 2,1226 | ||||
| + + + + + + | 2,0551 2,0734 2,0743 2,0568 2,0608 2,0858 |
Коэффициенты уравнения (3.97) вычислены по формулам, которые здесь не приводятся. В результате получено следующее уравнение регрессии второго порядка
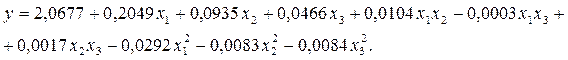 (3.96)
(3.96)
Дисперсия воспроизводимости вычислена по результатам шести опытов в центре плана sy2 = 0,00014576.
Дисперсии коэффициентов уравнения регрессии, имеют следующие значения:
s2{b0}=0,000024;
s2{bi}=0,00001064;
s2{bil}=0,00001822;
s2{bii}=0,00000966.
Обратим внимание, что они различны для линейных коэффициентов, эффектов. взаимодействия и квадратичных слагаемых уравнения (3.96)
Доверительные интервалы коэффициентов при 5% уровне значимости составили:
Δb0=±0,01264; Δbi=±0,008383; Δbil=±0,01097; Δbii=±0,00811.
Коэффициенты b12, b13, b23 по абсолютной величине меньше доверительного интервала, поэтому их можно считать статистически незначимыми и исключить из уравнения регрессии. После исключения незначимых коэффициентов уравнение (3.96) получило вид
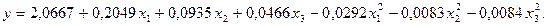 (3.97)
(3.97)
Проверка гипотезы адекватности модели, представленной уравнением (3.97), показала, что модель адекватна при 5%-ном уровне значимости, так как соотношение расчетного и табличного критериев Фишера свидетельствует в её пользу.
Fр<Fт.
Коэффициенты при квадратичных членах уравнения регрессии значимы. Это свидетельствует о том, что исследуемый процесс не может быть описан линейным уравнением. Уравнение (3.97) для рассматриваемой области изменения факторов дает возможность предложить другую модель процесса, которая получается подстановкой в уравнение (3.97) вместо кодированных натуральных значений факторов с использованием соотношения (3.95)
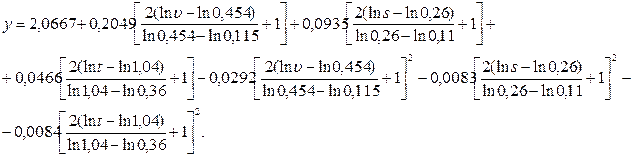
После преобразования получена зависимость
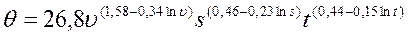 , (3.98)
, (3.98)
которая позволяет определять температуру резания в достаточно широком диапазоне изменения режимов резания при обработке точением стали 20.
По уравнению (3.98) построена номограмма, для быстрой оценки температуры резания в практических условиях.
Изложенная в примере методика планирования и обработки эксперимента может быть использована для определения температуры резания при механической обработке других конструкционных материалов.
Пример 3.Применение ротатабельного планирования второго порядка для минимизации шероховатости при обработке материалов резанием
Изготовление прецизионных деталей из пластмасс часто производится обработкой резанием. Выбор рациональных режимов резания в значительной степени определяет производительность процесса и качество обработанной поверхности. Предусматривалось изучения влияния режимов резания на шероховатость поверхности (параметр оптимизации) при обработке точением капролона и поиск условий, обеспечивающих минимальную шероховатость обработанной поверхности. Исследования проводились на высокоскоростном токарном станке. В качестве режущего инструмента использовались резцы с пластинками из твердого сплава ВК6М со следующими геометрическими параметрами: задний угол в плане 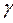 = 30°; передний угол в плане
= 30°; передний угол в плане 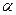 =18°; угол наклона режущей кромки
=18°; угол наклона режущей кромки 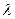 = 0; радиус скругления r = 1,5 мм. Шероховатость поверхностей режущего инструмента соответствовала Ra = 0,04
= 0; радиус скругления r = 1,5 мм. Шероховатость поверхностей режущего инструмента соответствовала Ra = 0,04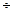 0,16 мкм. Обработке подвергались блоки из капролона без охлаждения.
0,16 мкм. Обработке подвергались блоки из капролона без охлаждения.
Шероховатость поверхности определялась на двойном микроскопе МИС-11. За критерий шероховатости принималась высота неровностей Rz,которая оценивалась осреднением по десяти измерениям каждого участка.
В качестве факторов, влияющих на шероховатость обрабатываемой поверхности, выбраны скорость резания V,подача S и глубина резания t, как параметры режима обработки, определяющие в основном высоту неровностей обработанной поверхности. В качестве параметра оптимизации принята высота неровностей.
На первом этапе исследования былпоставлен полный факторный эксперимент типа 23. Уровни факторов и интервалы варьирования выбраны по результатам предварительных поисковых экспериментов. Факторы, уровни и интервалы варьирования факторов приведены в табл. 3.7.
Матрица плана эксперимента и результаты измерений высоты неровностей у представлены в табл. 3.8.
\
Таблица 3.7.
| Фактор | Уровни фактора | Интервал варьирования | |||
| наименование, размерность | обозначение | верхний | основной | нижний | |
| скорость резания, м/мин | 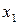 | ||||
| подача, мм/мин | 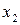 | 0,7 | 0,5 | 0,3 | 0,2 |
| глубина резания, мм | 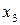 | 0,75 | 0,5 | 0,25 | 0,25 |
Таблица 3.8.
| Номер опыта | 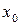 | 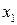 | 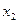 | 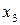 | 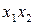 | 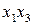 | 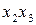 | 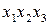 | y (Rz) |
| + | - | - | - | + | + | + | - | 2,16 | |
| + | + | - | - | - | - | + | + | 2,65 | |
| + | - | + | - | - | + | - | + | 3,80 | |
| + | + | + | - | + | - | - | - | 4,70 | |
| + | - | - | + | + | - | - | + | 2,22 | |
| + | + | - | + | - | + | - | - | 2,48 | |
| + | - | + | + | - | - | + | - | 4,20 | |
| + | + | + | + | + | + | + | + | 4,89 |
План эксперимента типа 23 позволяет получить раздельные оценки для коэффициентов уравнения регрессии вида
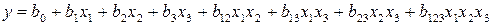 . (3.83)
. (3.83)
В результате расчетов получены следующие значения коэффициентов
b0 = 3,3875; b1 = 0,2925; b 2 = 1,01; b3 = 0,06;
b12 = 0,105; b13 = - 0,055; b23 = 0,0875; b123 = 0,0025.
После подстановки значений коэффициентов уравнение (3.83) приняло вид
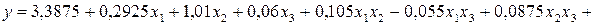
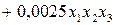 . (3.84)
. (3.84)
Для проверки адекватности полученного уравнения и определения дисперсий коэффициентов определяется дисперсия воспроизводимости эксперимента 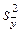 по результатам шести параллельных опытов, поставленных в центре плана (опыты 1
по результатам шести параллельных опытов, поставленных в центре плана (опыты 1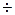 6, табл. 3.9).
6, табл. 3.9).
Таблица 3.9.
| Опыты | Номер опыта | 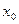 | 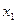 | 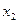 | 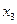 | 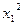 | 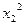 | 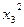 | y |
| центр плана | + + + + + + | 2,31 2,08 2,12 2,32 2,36 2,12 | |||||||
| «звёздные» точки | + + + + + + | -1,682 +1,682 | -1,682 +1,682 | -1,682 +1,682 | 2,828 2,828 | 2,828 2,828 | 2,828 2,828 | 3,55 4,50 1,80 5,15 2,32 2,56 |
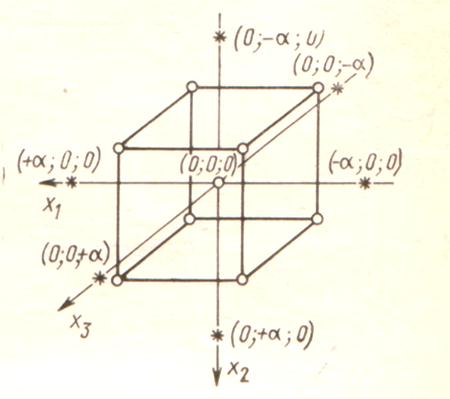
Рис.3.4. Центральный композиционный план для трёх факторов.
Среднее арифметическое значение параметра 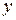 в центре плана равно
в центре плана равно 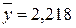 . Дисперсиявоспроизводимости эксперимента
. Дисперсиявоспроизводимости эксперимента 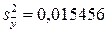 . Разность между значением параметра
. Разность между значением параметра 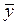 в центре плана и значением свободного члена b0 (в центре плана значения всех эффектов в уравнении (93) равно нулю) составляет по модулю
в центре плана и значением свободного члена b0 (в центре плана значения всех эффектов в уравнении (93) равно нулю) составляет по модулю 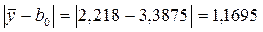 .
.
Полученная разность во много раз превышает ошибку эксперимента (дисперсию воспроизводимости) 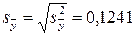 . Из этого следует, что коэффициенты при квадратичных членах значимо отличаются от нуля, а исследуемая зависимость не может быть с достаточной точностью аппроксимирована уравнением (3.100). В связи с этим необходимо перейти к модели более высокого порядка. Предположим, что явление описывается моделью второго порядка, т.е. полиномом вида
. Из этого следует, что коэффициенты при квадратичных членах значимо отличаются от нуля, а исследуемая зависимость не может быть с достаточной точностью аппроксимирована уравнением (3.100). В связи с этим необходимо перейти к модели более высокого порядка. Предположим, что явление описывается моделью второго порядка, т.е. полиномом вида
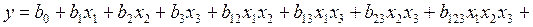

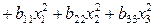 . (3.85)
. (3.85)
Эксперимент был поставлен по программе центрального композиционного ротатабельного планирования второго порядка. Реализованные восемь опытов полного факторного эксперимента 23 (см. табл. 22) и шесть опытов в центре плана (см. табл. 3.13) дополнили шестью опытами в «звездных» точках (опыты 7 12, табл. 3.13). Величина «звездного» плеча
12, табл. 3.13). Величина «звездного» плеча 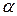 в рассматриваемом случае равна 1,682.
в рассматриваемом случае равна 1,682.
Получили следующие значения коэффициентов:
b0 = 2,1956; b1 = 0,2882; b2 = 0,9819; b3 = 0,0646; b12 = 0,105; b13= - 0,055; b23 = 0,0875; b123 = 0,0025; b11 = 0,6663; b22 = 0,4594; b33= 0,0833.
После подстановки значений коэффициентов в уравнение 3.101) оно получило вид
y= 2,1956 + 0,2882 х1 + 0,9819 х2 + 0,0646 х3 + 0,105 х1х2 - 0,055 х1х3 +
+ 0,0875 х2х3 + 0,0025 х1х2 х3+ 0,6663 х12 + 0,4594 х22+ 0,083 х32. (3.102)
После нахождения дисперсий коэффициентов и их доверительных интервалов получено что коэффициенты b3 , b12, b13, b23, b123 , b33 по абсолютной величине меньше соответствующих доверительных интервалов их определения, то можно признать их статистически незначимыми и исключить из уравнения регрессии. Так как среди незначимых коэффициентов оказался также коэффициент b 33при квадратичном члене, то значимые коэффициенты при других эффектах должны быть пересчитаны, например, с использованием МНК. Пересчитанные значения коэффициентов приведены ниже:
b0 = 2,26; b11 = 0,6555; b22 = 0,4389; b1 = 0,2882; b2 = 0,9819.
Таким образом, математическая модель, полученная в результате ротатабельного планирования второго порядка, приняла вид
у=2,26+ 0,2882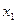 + 0,9819
+ 0,9819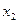 + 0,6555
+ 0,6555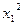 +0,438
+0,438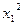 . (3.103)
. (3.103)
Для проверки адекватности модели найдена дисперсия Sад2 адекватности и остаточная сумма квадратов, о также определено расчетное значение F-критерия:
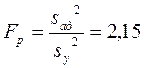
При 5%-ном уровне значимости и числах степеней свободы для числителя 10 и знаменателя 5 табличное значение критерия Fт равно 4,74. Значение FР<Fт, поэтому модель (3.103) следует признать адекватной. Уравнение (3.103) неудобно для интерпретации полученных результатов и практических расчетов, поэтому оно преобразовано по формулам перехода от кодированных значений (х1, х2, х3) к натуральным значениям факторов скорость резания, подача и глубина резания (u,s,t):
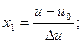
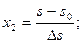
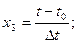
Где 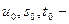 натуральные значения факторов на основных уровнях;
натуральные значения факторов на основных уровнях; 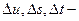 значения интервалов варьирования.
значения интервалов варьирования.
Таким образом,
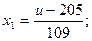
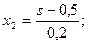
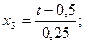
Уравнение (3.103) с учетом отношений (3.104) можно представить следующим выражением:
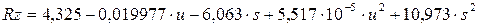 (3.105)
(3.105)
Из приведенного выражения следует, что в области эксперимента (t = 0,25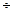 0,75 мм) глубина резания не оказывает влияния на шероховатость обработанной поверхности капролона. Уравнение (3.103) использовано для поиска оптимального режима обработки капролона резцом с заданной геометрией (вторая задача планирования эксперимента, см. параграф 3.1)
0,75 мм) глубина резания не оказывает влияния на шероховатость обработанной поверхности капролона. Уравнение (3.103) использовано для поиска оптимального режима обработки капролона резцом с заданной геометрией (вторая задача планирования эксперимента, см. параграф 3.1)
В результате переноса начала координат в центр фигуры с координатами х1s= -0,22; х2s = = -1,12 (они соответствуют значениям u=181 м/мин; s= 0,276 мм/об) и поворота координатных осей уравнение (3.103) было приведено к каноническому виду
Y- 1,68 = 0,6555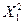 + 0.4389
+ 0.4389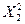 . (3.106)
. (3.106)
Выражение (99) является уравнением эллипса в каноническом виде. Так как коэффициенты B11 и B22имеют положительные знаки, центр эллипса
(х1s = -0,22; х2s = -1,12) является минимумом функции отклика. В этом случае для поиска экстремума достаточно поставить опыт в центре фигуры и проверить, насколько точно значение параметра оптимизации, предсказанное уравнением регрессии, совпадает с экспериментальным.
В дополнительном опыте, поставленном в центре фигуры (х1s = -0,22;
х2s = -1,12), получено значение функции отклика у = 1,7 мкм. Дальнейшее варьирование скорости и подачи вблизи экстремума не вызвало уменьшения значения y. Таким образом, оптимальным следует считать режим обработки:
у = 181 м/мин, s= 0,276 мм/об при t= 0,25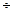 0,75 мм.
0,75 мм.
Уравнение (3.106) можно также использовать для определения ожидаемой шероховатости поверхности при обработке капролона на режимах, входящих в область эксперимента.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ к разделу 3
Для закрепления материала раздела 3 предлагается ответитьна контрольные вопросы и решить задачи по планированию экспериментальных исследований.
Контрольные вопросы:
1. Основные виды эксперимента.
2. Ошибки опытов. Дисперсия воспроизводимости.
3. Две задачи ПЭ. Тенденции ПЭ.
4. Основные понятия ПЭ. Требования к объекту исследования и
факторам.
5. Математические модели объекта.
6. Предварительный этап планирования эксперимента. Натуральная и кодированная системы координат.
7. Полный факторный эксперимент. Пример ПФЭ.
8. Свойства планов ПФЭ.
9. Метод наименьших квадратов и методика получения оценок коэффициентов линейной однофакторной модели.
10. Матричный подход в ТПЭ. Формула для вычисления коэффициентов линейных моделей по планам ПФЭ.
11. Статистические свойства коэффициентов. Методика оценки значимости коэффициента регрессионной модели.
12. Дробный факторный эксперимент. Генерирующее соотношение. Определяющий контраст.
Задачи:
1. Составьте матрицу ПФЭ для четырехфакторного эксперимента.
2. Определите коэффициенты линейной двухфакторной модели вида y=b0+b1X1+b2X2 если получены следующие значения функции отклика
| № опыта | X1 | X2 | y |
| +1 | +1 | ||
| -1 | +1 | 2,5 | |
| +1 | -1 | ||
| -1 | -1 | -5,5 |
3. Проверьте значимость коэффициентов линейной модели идентифицированной по плану ПФЭ 2, если коэффициент Стьюдента равен I,8 а b0= 5, b 1=0,3, b2= 3. Дисперсия воспроизводимости равна 0,25.
4. Разберите пример на стр. 34 – 37 в источнике [12].
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 2
 2014-02-13
2014-02-13 3837
3837