2014-02-13
1015
Лекция 12
Рассмотрим центральный симметричный композиционный план с одной точкой в центре плана и 2К - "звездных" точек. Преобразуем полином второго порядка к виду
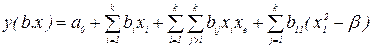
Здесь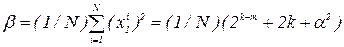 
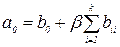
N = 2k-m + 2k+l- общее число точек плана.
Матрица F для выбранного плана и преобразованной модели примет вид (табл. 7.1).
Таблица 7.1.
| № опыта | Для а0 | Для bi | Для bij | Для bii | |||||||
| x1 | x2 | … | xk | x1x2 | … | xk-1xk |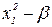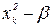 
| … | 
| ||
| Я 1 | +1 | +1 | … | +1 | +1 | … | +1 |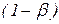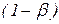 
| … |
| |
| Д 2 | -1 | +1 | … | +1 | -1 | … | +1 |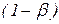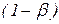
| … |
| |
| Р. | . | . | . | … | . | . | … | . | . | … | . |
| О 2k-m | -1 | -1 | … | -1 | +1 | … | +1 |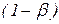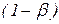
| ... |
| |
| 2k-m +1 |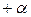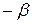 
| … | … | 
| … | 
| |||||
| З +2 |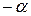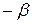 
| … | … |
| … |
| |||||
| В т +3 |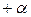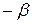
| … | … |
| … | . | |||||
| Е о +4 |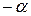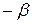
| … | … |
| … | . | |||||
| Д ч. | . | . | . | … | . | . | … | . | . | … | . |
| Н к. | . | . | . | … | . | . | … | . | . | … | . |
| Ы и. | . | . | . | … | . | . | … | . | . | … | . |
| Е +2k | … |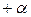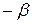
| … |
| … |
| |||||
| … |
| … |
| … |
| ||||||
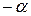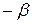| Центр плана | … | … | … |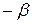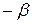
| … |
|
Рассмотрим элементы информационной матрицы: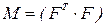 
. Они равны скалярному произведению столбцов матрицы F и равны нулю при любом 
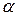для всех пар столбцов за исключением скалярного произведения столбцов при квадратичных функциях вида 
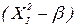, значения которых зависит от .
|
|
|
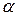Можно показать, что при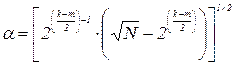 
скалярные произведения столбцов при квадратичных функциях также будут равны нулю [1]. Информационная матрица примет вид
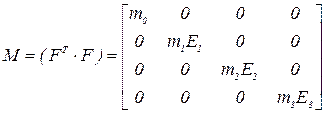
Здесь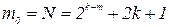 
; 
; 
; 
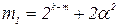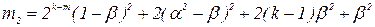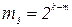; E1, E2 - единичные матрицы размера k, E3 - единичная матрица размера k(k-l)/2. Дисперсионная матрица 
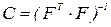будет
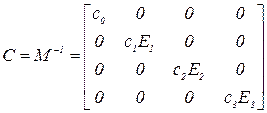где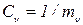 
, 
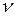=0,...,k.
Отсюда можно получить формулы для расчета коэффициентов:
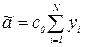
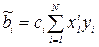I=1,…,k
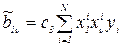I=1,…,k, 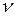=1,…,k,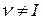 
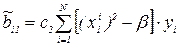I=1,…,k
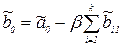
Дисперсии оценок коэффициентов равны:
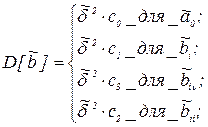I=1,…,k;
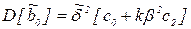
Величина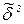 
есть оценка дисперсии ошибок наблюдений, которая
может быть получена, как и ранее, по результатам n0 наблюдений в центральной точке плана. Так как информационная матрица, полученная при указанном значении 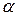, является диагональной, то соответствующий ЦКП ортогональный, а следовательно, и все коэффициенты оцениваются независимо. Для оценки, значимости коэффициентов и адекватности модели может применяться обычный подход (см. п. п., 4.3. 4.4).
При построении ЦКП следует иметь в виду, что в качестве ядра можно использовать только такой план, который позволяет получать не смешанные друг с другом оценки коэффициентов при парных взаимодействиях. Разрешающая способность плана должна быть не ниже пяти. При числе переменных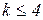 
это условие для ДФП не выполняется, поэтому их использование в качестве ядра плана невозможно. При k=5 в t качестве ядра можно использовать ДФП вида 25-1 (полуреплику) с генерирующим соотношением Х5=Х1Х2Х3Х4. Аналогично для k=6, 7. Для к=8 и более уже можно использовать четвертьреплики.
|
|
|
