ОПРЕДЕЛИТЕЛИ И ПРАВИЛО КРАМЕРА
ЛЕКЦИЯ 2
Изменение формата и количества полос
Как число колонок на газетной полосе во многом определяет ее план и верстку, так и количество полос в номере диктует его содержание и оформление. Чем больше полос в газете, тем больше вариантов размещения материалов — свободного распределения по страницам или закрепления на постоянном месте на одних и тех же полосах. Поэтому, используя взаимозависимость форматов газет, в некоторых редакциях предпочитают увеличивать количество полос в номере за счет уменьшения формата: это дает дополнительные возможности для планирования и оформления газеты.
К уменьшению или увеличению формата газеты и количества ее полос прибегают также и в тех случаях, когда хотят выделить какой-либо номер, привлечь к нему внимание читателя. Это нередко делают при выпуске специальных (праздничных, целевых, тематических) номеров.
Возможен даже выпуск газетного номера с разноформатными полосами. Этот прием используется, например, при публикации так называемой газеты в газете (подробнее об этом мы расскажем в следующих номерах журнала). Стремясь выделить какойлибо постоянный раздел газеты, редакция может напечатать его в виде нескольких тематических полос, отличных от постоянного формата номера.
Определители и правило Крамера. Определители 2-го и 3-го порядка. Правило Крамера. Миноры и алгебраические дополнения. Разложение определителя по строке или столбцу. Основные свойства определителей Метод элементарных преобразований.
Понятие определителя возникло также в связи с задачей решения систем линейных уравнений. Определитель (или детерминант) есть число, характеризующее квадратную матрицу A и обозначается обычно символами: det A, | A | или D. Если матрица задана явно, в виде таблицы, то определитель обозначают, заключая таблицу в вертикальные линии.
Определитель матрицы второго порядка находится следующим образом:

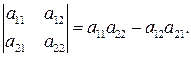 (2.1)
(2.1)
Он равен произведению элементов главной диагонали матрицы минус произведение элементов второй диагонали.
Например, 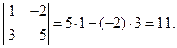 à
à
Следует еще раз подчеркнуть, что матрица есть таблица чисел, тогда как определитель есть число, определяемое через элементы квадратной матрицы.
Рассмотрим теперь систему двух линейных уравнений с двумя неизвестными:
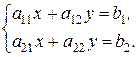
Используя понятие определителя 2-го порядка, решение этой системы можно записать в виде:
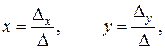 (2.2)
(2.2)
где
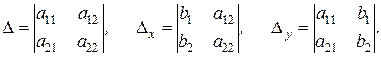
Это есть правило Крамера решения системы двух линейных уравнений с двумя неизвестными при условии, что D¹0.
Пример 2.1. Решить систему линейных уравнений, используя правило Крамера:
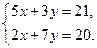
Решение. Найдем определители:
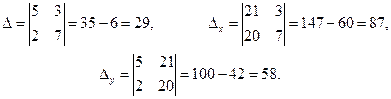
Отсюда
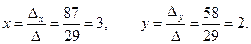 â
â
Историческая справка. Идея понятия «определителя» могла бы принадлежать Г. Лейбницу (1646-1716), если бы он развил и опубликовал свои идеи относительно определителей, к которым он пришел в 1693 г. Поэтому приоритет в разработке метода определителей решения систем линейных уравнений принадлежит Г. Крамеру (1704-1752), который опубликовал свои исследования по этой теме в 1750 г. Однако Крамер не построил полноценной теории определителей, к тому же ему не доставало удобного обозначения. Первое обширное исследование, посвященное определителям, было А. Вандермондом (1735-1796) в 1772 г. Он дал логическое изложение теории определителей и ввел правило разложения определителя с помощью миноров. Полное изложение теории определителей было дано лишь в 1812 г.
Ж. Бине (1786-1856) и О. Коши (1789-1858). Термин «определитель» («детерминант») в современном его значении был введен Коши (ранее этот термин использовался К. Гауссом для обозначения дискриминанта квадратичной формы).
 2014-02-13
2014-02-13 1571
1571







