Определители n-го порядка

Дополнительным минором M_ij элемента a_ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A_ij элемента a_ij называется минор этого элемента, взятого со знаком (–1) ^i+j, т.е. A_ij = (–1) ^i+jM_ij.

Например, найдем миноры и алгебраические дополнения элементов a ₂₃ и a ₃₁ определителя

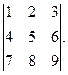
Получаем

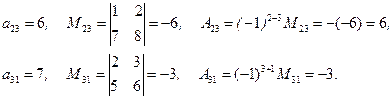à

Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n-го порядка по строке или столбцу.

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

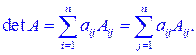(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка. В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

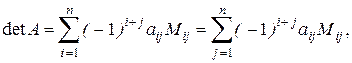
т.е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.

;

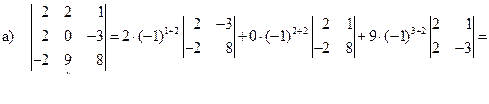
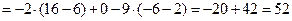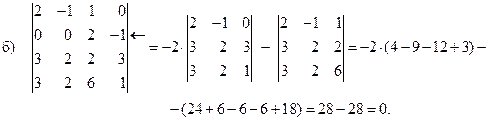à