Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство 1. Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы:
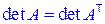 .
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2. Определитель меняет знак при перестановке двух строк (столбцов).
Следствие. Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3. Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя.
Например,
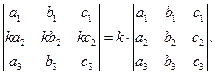
Следствие. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
Свойство 4. Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число.
Например,
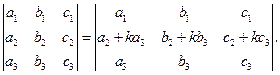
Свойство 5. Определитель произведения матриц равен произведению определителей матриц:
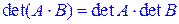 .
.
 2014-02-13
2014-02-13 2910
2910