Таблица 1.37
| x1 | x2 | x3 | ... | xn | ||
| y1 | a11 | a12 | a13 | ... | a1n | b1 |
| y2 | a21 | a22 | a23 | ... | a2n | b2 |
| y3 | a31 | a32 | a33 | ... | a3n | b3 |
| ... | ... | ... | ... | ... | ... | ... |
| ym | am1 | am2 | am3 | ... | amn | bm |
| c1 | c2 | c3 | ... | cn |
Например, чтобы получить первое ограничение двойственной задачи, следует найти сумму произведений чисел, стоящих в столбце под x1, на соответствующие переменные первого столбца:
a11y1 + a21y2 +... + am1ym.
Полагаем, что эта сумма не меньше c1:
a11y1 + a21y2 +... + am1ym 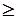 c1.
c1.
Аналогично составляют и остальные ограничения для двойственной задачи. При этом устанавливают такие соответствия:
а) переменной x1 исходной задачи соответствует первое ограничение двойственной задачи, переменной x2 - второе ограничение двойственной задачи и т.д., переменной xn - последнее ограничение двойственной задачи, и наоборот;
б) переменной y1 двойственной задачи соответствует первое ограничение исходной задачи и т.д., переменной ym двойственной задачи соответствует последнее ограничение исходной задачи и наоборот.
Выражение для целевой функции получается как сумма произведений переменных первого столбца на соответствующие числовые значения последнего столбца.
Если система ограничений исходной задачи на нахождение max, кроме неравенств типа 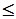 , содержит неравенства типа
, содержит неравенства типа 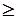 , то перед построением двойственной задачи левые и правые части неравенств типа
, то перед построением двойственной задачи левые и правые части неравенств типа 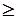 необходимо умножить на -1. А в задаче на нахождение min, умножаем на -1 неравенства типа
необходимо умножить на -1. А в задаче на нахождение min, умножаем на -1 неравенства типа 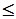 . Если в исходной задаче имеются ограничения, заданные равенствами, то каждое из них заменяется двумя ограничениями - неравенствами, а затем в зависимости от типа задачи поступают так, как сказано выше.
. Если в исходной задаче имеются ограничения, заданные равенствами, то каждое из них заменяется двумя ограничениями - неравенствами, а затем в зависимости от типа задачи поступают так, как сказано выше.
Пример. Пусть в систему ограничений исходной задачи на max входит уравнение
2 x 1 + 4 x 2 + 3 x 3 = 10.
2 x 1 + 4 x 2 + 3 x 3 = 10.
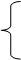 откуда 2 x 1 + 4 x 2 + 3 x 3
откуда 2 x 1 + 4 x 2 + 3 x 3 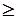 10, (1.65)
10, (1.65)
2 x 1 + 4 x 2 + 3 x 3 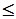 10.
10.
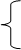 тогда - 2 x 1 - 4 x 2 - 3 x 3
тогда - 2 x 1 - 4 x 2 - 3 x 3 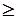 - 10, (1.66)
- 10, (1.66)
2 x 1 + 4 x 2 + 3 x 3 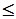 10.
10.
Уравнение (1.63) в системе ограничений исходной задачи на max должны быть типа 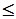 , а в задаче на min - типа
, а в задаче на min - типа 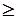 .
.
В теории ЛП [ 1, 2 ] доказываются следующие теоремы.
Теорема 1. Если одна из задач двойственной пары имеет оптимальное решение, то другая задача также имеет решение, причем max целевой функции исходной задачи и min целевой функции двойственной задачи числено равны. Если же одна из задач не имеет оптимального решения, то система ограничений двойственной задачи противоречива.
Теорема 2. (теорема равновесия). Если в оптимальном плане исходной задачи значение какой-либо переменной строго больше нуля, то соответствующее ограничение двойственной задачи при подстановке в него оптимального плана становится равенством. Наоборот, если некоторое ограничение оптимального плана обращается в строгое неравенство, то соответствующее значение переменной решения исходной задачи обращается в нуль.
Сформулированные теоремы двойственности находят широкое практическое применение. Эти теоремы позволяют, например, решение задачи ЛП (которое по той или иной причине вызывает затруднение при реализации) свести к решению двойственной задачи. Например, если матрица A прямоугольная и сильно “вытянута”, то переход от прямой задачи к двойственной может дать значительный эффект.
Такое сведение особенно полезно и выгодно, если число ограничений исходной задачи велико и значительно превышает число переменных.
Заметим, что объем вычислений в задачах ЛП при использовании симплекс-метода для решения определяется количеством ограничений.
Теоремы двойственности справедливы как для симметричных, так и несимметричных двойственных задач.
Пример. К двум станциям отправления A и B прикреплены три станции назначения (I, II, III).
Ежедневно из станций отправления вывозится 65 т груза, в том числе со станции A - 40 т, а из B - 25 т. На станции назначения должны поступать следующие количества грузов: I - 10 т, II - 35 т, III - 20 т. Расстояния от станций A и B до соответствующих станций назначения даны в табл. 1.38.
 2014-02-09
2014-02-09 663
663