Таблица 1.43
Таблица 1.42
Таблица 1.41
Таблица 1.40
Тогда
Таблица 1.39
| x11 | x12 | x13 | x21 | x22 | x23 | ||
| U1 | |||||||
| U2 | |||||||
| V1 | |||||||
| V2 | |||||||
| V3 | |||||||
| C |
Тогда двойственная задача формулируется так:
максимизировать целевую функцию
F* = 40U1 + 25U2 + 10V1 + 35V2 + 20V3
|
U1 + V1  7,
7,
U1 + V2  2,
2,
U1 + V3  4,
4,
U2 + V1  3,
3,
U2 + V2  8,
8,
U2 + V3  9.
9.
Заметим, что все ограничения исходной задачи имеют вид равенств, поэтому все переменные двойственной задачи (U1, U2, V1, V2, V3) могут принимать отрицательные значения.
Напомним, что математическая модель (прямой) транспортной задачи имеет вид
F = 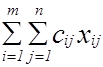
 min
min
при условиях
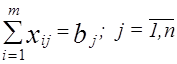 .
.
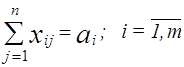 .
.
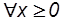 .
.
Математическая модель двойственной транспортной задачи в общем виде имеет вид
F* = 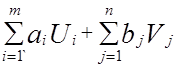 ® max
® max
при условиях (в координатной форме)
 U1 + V1
U1 + V1  C11,
C11,
U1 + V2  C12,
C12,
......
U1 + Vn  C1n,
C1n,
U2 + V1  C21,
C21,
U2 + V2  C22,
C22,
......
U2 + Vn  C2n,
C2n,
......
Um + V1  Cm1,
Cm1,
......
Um + Vn  Cmn.
Cmn.
Пример. Для построения прямой задачи, состоящей в определении max целевой функции:
F =2 x1 +7 x2  max
max
при ограничениях
|
 14, (I)
14, (I)
x 1 + x 2  8, (II)
8, (II)
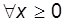
составить двойственную задачу и найти решение обеих задач.
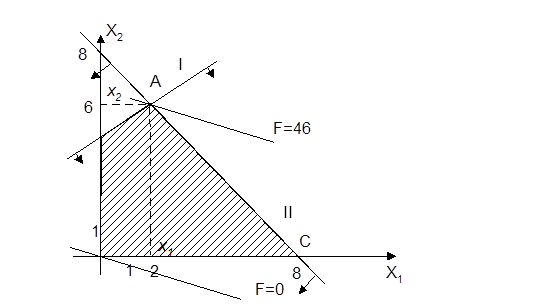
Рис. 1.14
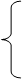 Пользуясь вспомогательной таблицей, приведенной выше, записываем ограничение двойственной задачи:
Пользуясь вспомогательной таблицей, приведенной выше, записываем ограничение двойственной задачи:
|
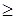 2, (III)
2, (III)
3y1 + y2 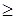 7, (IV)
7, (IV)
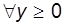 ;
;
целевая функция, по определению двойственной задачи, имеет вид
F* = 14y1 + 8y2  min.
min.
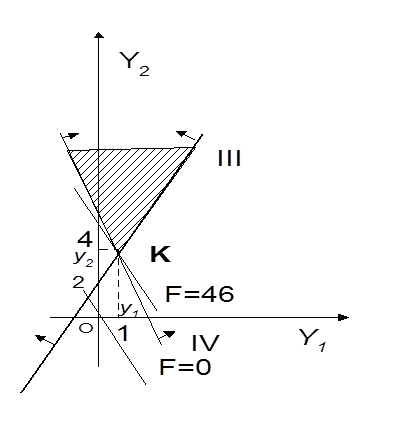
Рис. 1.15
Поскольку в обеих задачах число неизвестных равно двум, их решение может быть выполнено графически (рис. 1.14 и рис. 1.15).
В прямой задаче max целевой функции достигается в точке A (X1 = 2; X2 = 6) (рис. 1.14).
Минимальное значение целевая функция F* двойственной задачи принимает в точке K (рис. 1.15). Следовательно, Y*1 = 1, Y*2 = 4 - оптимальный план двойственной задачи и F*min = 46.
Итак, значения целевых функций прямой и двойственных задач при их оптимальных планах числено равны между собой.
Пример. Найти решение двойственной пары задач.
Прямая задача:
F = x1 + 14x2 + 13x3 + 12x4  min
min
при ограничениях
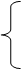 - 3 x1 + x2 + 2 x3 + 3 x4
- 3 x1 + x2 + 2 x3 + 3 x4 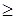 1,
1,
2 x1 + 2 x2 + x3 - x4 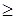 1,
1,
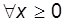 .
.
 С учетом сделанных выше замечаний двойственная задача будет иметь вид
С учетом сделанных выше замечаний двойственная задача будет иметь вид
- 3y1 + 2y2  1,
1,
y1 + 2y2  14,
14,
2y1 + y2  13,
13,
3y1 - y2  12.
12.
F* = y1 + y2  max.
max.
 Будем решать эти задачи с помощью симплекс-метода. Для этого приведем ограничение и целевую функцию двойственной задачи к основному виду:
Будем решать эти задачи с помощью симплекс-метода. Для этого приведем ограничение и целевую функцию двойственной задачи к основному виду:
y3 = 1 - (- 3y1 + 2y2),
y4 = 14 - (y1 + 2y2),
y5 = 13 - (2y1 + y2),
y6 = 12 - (3y1 - y2).
F* = 0 - (- y1 - y2 )  max.
max.
Для записи прямой задачи в симплексную таблицу двойственной задачи преобразуем эту прямую задачу таким образом:
 - 3 x1 + x2 + 2 x3 + 3 x4 - x5 = 1,
- 3 x1 + x2 + 2 x3 + 3 x4 - x5 = 1,
2 x1 + 2 x2 + x3 - x4 - x6 = 1.
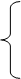 x5 = - 1 - [ (- 3)(- x1) + 1(- x 2 ) + 2(- x3) + 3(- x 4 ) ],
x5 = - 1 - [ (- 3)(- x1) + 1(- x 2 ) + 2(- x3) + 3(- x 4 ) ],
x6 = - 1 - [ 2(- x1) + 14(- x2) + 1(- x 3 ) - 1(- x4) ],
F = 0 - [ 1(- x1) + 14(- x 2 ) + 13(- x3) + 12(- x 4 ) ]  min.
min.
Далее записываем обе задачи в двойственную симплекс-таблицу (табл. 1.40).
| x баз | x5 | x6 | B y | |
| y баз | y1 | y2 | F | |
| - x1 | y3 | -3 | ||
| - x2 | y4 | |||
| - x3 | y5 | |||
| - x4 | y6 | - 1 | ||
| Bx | F | - 1 | - 1 |
Опуская промежуточные таблицы, запишем последнюю таблицу (табл. 1.41)
| x баз | x2 | x3 | B y | |
| y баз | y4 | y5 | F | |
| - x1 | ||||
| - x5 | ||||
| - x6 | ||||
| - x4 | ||||
| Bx | F | 1/3 | 1/3 |
Из этой таблицы находим решение двойственной пары:
max F = 9; min F = 9;
y4 = 0; y5 = 0; y3 = 3; y1 = 4; y2 = 5; y6 = 5.
x1 = 0; x 5 = 0; x 6 = 0; x 4 = 0; x 2 = 1/3; x 3 = 1/3.
Окончательно прямая задача имеет следующее решение:
max F = 9;
x1 = 0; x 2 = 1/3; x 3 = 1/3; x 4 = 0.
В заключение рассмотрим экономическую интерпретацию двойственных задач.
Пример [ 7 ].Для производства трех видов изделий A, B и C используются три различных вида сырья. Каждый из видов сырья может быть использован в количестве соответственно не больше 180, 210 и 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции каждого вида приведены в
табл. 1.42.
| Вид сырья | Нормы затрат сырья на единицу продукции | ||
| A | B | C | |
| I | |||
| II | |||
| III | |||
| Цена единицы продукции |
Обозначим через x 1 число производимых изделий A, x 2 - изделий B, x 3 - изделий C.
Тогда целевая функция будет: F = 10 x1 + 14 x2 + 12 x3  max
max
 при ограничениях
при ограничениях
4 x1 + 2 x2 + x3  180,
180,
3 x1 + x2 + 3 x3  210,
210,
x1 + 2 x2 + 5 x3  244,
244,
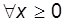 .
.
Это прямая задача.
Составим двойственную задачу, для чего запишем каждому из видов сырья, используемого для производства продукции, двойственную оцен-ку, соответственно равную y1, y2 и y3. Тогда общая оценка сырья, используемого на производство продукции, будет
F* = 180y1 + 210y2 + 244y3  min.
min.
По условию задачи двойственные оценки должны быть такими, чтобы общая оценка сырья, использованного на производство единицы продукции каждого вида, была не меньше цены единицы продукции данного вида:
 4 y1 + 3y 2 + y3
4 y1 + 3y 2 + y3 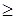 10,
10,
2y 1 + y2 + 2y 3 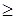 14,
14,
y 1 + 3y 2 + 5y 3 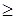 12,
12,
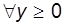 .
.
Чтобы найти решение этих задач, следует отыскать решение какой-либо одной из них. Находим решение прямой задачи. Опуская выкладки, имеем: оптимальным планом производства изделий является такой, при котором изготовляется 82 изделия B и 16 изделий C. При этом остается неиспользованным 80 кг сырья II вида, а общая стоимость составляет F = 1340 усл. ед.
Решение двойственной задачи дает следующие результаты:
y * 1 = 23/4; y* 2 = 0; y*3=5/4; F* =1340.
Переменные y * 1 и y * 3 обозначают условные двойственные оценки единицы сырья I и III видов соответственно. Эти оценки отличны от нуля, а сырье I и III видов полностью используется при оптимальном плане производства продукции. Двойственная оценка единицы сырья II вида равна нулю. Этот вид сырья не полностью используется при оптимальном плане производства продукции.
Таким образом, положительную двойственную оценку имеют лишь те виды сырья, которые полностью используются при оптимальном плане производства изделий.
Следовательно, двойственные оценки определяют дефицитность используемого предприятием сырья.
Подставим оптимальные значения двойственных оценок в систему ограничений двойственной задачи и получим
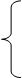 23 + 5/4 > 10,
23 + 5/4 > 10,
23/2 + 5/2 = 14,
23/4 + 25/4 = 12.
Первое ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственная оценка сырья, используемого на производство одного изделия A, выше цены этого изделия, поэтому выпускать изделие A невыгодно.
Второе и третье ограничения двойственной задачи выполняются как строгие равенства, что означает: двойственные оценки сырья, используемого для производства единицы соответственно B и C, равны в точности их ценам. Значит, их выпуск экономически целесообразен. Их производство и предусмотрено оптимальным планом прямой задачи.
В заключение заметим, что модель ЛП можно рассматривать и с других позиций - как модель, описывающую взаимосвязь между “входом” и “выходом” некоторой системы. Потребляемые ресурсы характеризуют вход системы, а получаемая прибыль соответствует выходу. Система
остается в нестабильном состоянии до тех пор, пока вход превышает выход. Устойчивое состояние системы достигается при равенстве прибыли общей ценности ресурсов.
С учетом выше сказанного, приведенная ранее, табл. 1.37 для задания двойственных задач, может иметь вид (табл. 1.43).
| Производительность | ||||||||||
| C1 | C2 | C3 | ... | Cj | ... | Cn | ||||
| Век- | y1 | a11 | a12 | a13 | ... | a1j | ... | a1n | b1 | Ре- |
| тор | y2 | a21 | a22 | a23 | ... | a2j | ... | a2n | b2 | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | сур- | |
| оце- | yi | ai1 | ai2 | ai3 | ... | aij | ... | ain | bi | |
| нок | ... | ... | ... | ... | ... | ... | ... | ... | ... | сы |
| ym | am1 | am2 | am3 | ... | amj | ... | amn | bm | ||
| x1 | x2 | x3 | ... | xj | ... | xn | ||||
| План производства |
Постройте математические модели двойственных задач по отношению к следующим задачам:
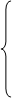
1. X1 + 3X3 - 4X5 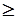 8,
8,
X1 - 2X2 + X3 + 3X4 - 2X5 = 6,
2X1 + 3X2 - 2X3 - X4 + X5 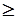 4,
4,
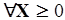 ,
,
F = X1 - 2X2 + X3 - X4 + X5  min.
min.
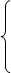 2. X1 - 2X2 + 3X4 + X5 = 8,
2. X1 - 2X2 + 3X4 + X5 = 8,
X1 + X3 + X4 - 2X5 = 6,
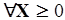 ,
,
F = - 2X2 + X4 + 3X5  max.
max.
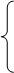 3. X1 - 2X2 + X4 = 8,
3. X1 - 2X2 + X4 = 8,
X1 + X3 - 3X4 = 6,
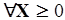 ,
,
F = - 3X2 - X4  max.
max.
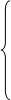 |
4. 2X1 - X2 + X3 - 3X4 - X5 = 10,
X1 + 2X2 - X3 + 2X4 + X5 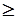 8,
8,
2X1 - X2 + 3X3 - X4 + 2X5  4,
4,
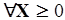 ,
,
F = 2X1 - X2 + X3 - 3X4 + X5  min.
min.
В следующих задачах дайте геометрическую интерпретацию исходной и двойственных задач и найдите оптимальное решение для разрешимых задач:
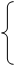 5. - X1 + 3X2
5. - X1 + 3X2  6,
6,
3X1 - X2  6,
6,
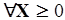 ,
,
F = X1 + X2  max.
max.
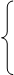 6. - 2X1 + X2
6. - 2X1 + X2  2,
2,
X1 - X2  2,
2,
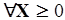 ,
,
F = 2X1 + X2  max.
max.
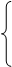 7. 3X1 - X2
7. 3X1 - X2 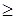 1,
1,
- X1 + 3X2  5,
5,
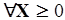 .
.
F = 2X1 + X2  min
min
 8. - X1 + 2X2 + X3 = 4,
8. - X1 + 2X2 + X3 = 4,
X1 - X2 + X4 = 3,
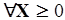 .
.
F = 3X1 + X2  max
max
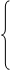 9. X1 - X2
9. X1 - X2  1,
1,
X1 - X2 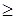 1,
1,
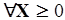 ,
,
F = X1 - X2  max.
max.
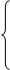 |
10. 3X1 + 5X2 + X3 + X4 = 32,
X1 - 3X2 - X3 + X4 = - 8,
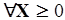 .
.
F = 3X1 - X2 - X3 + X4  max.
max.
Найдите решение двойственной задачи, используя решение исходной задачи, полученное симплекс-методом:
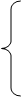 11. - X1 + X2 + X3 = 1,
11. - X1 + X2 + X3 = 1,
X1 - X2 + X4 = 1,
X1 + X2 + X5 = 2.
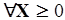 .
.
F = 2X1 - X2 + 3X3 - 2X4 + X5  max.
max.
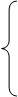 12. X1 + 2X2 - X3 + X4 = 0,
12. X1 + 2X2 - X3 + X4 = 0,
2X1 - 2X2 + 3X3 + 3X4 = 9,
X1 - X2 + 2X3 - X4 = 0.
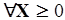 .
.
F = - 3X1 + X2 + 3X3 - 34X4  min.
min.
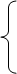 13. 5X1 + 12X2 + 2X3 = 9,
13. 5X1 + 12X2 + 2X3 = 9,
3X1 + 10X2 + 4X3 = 11,
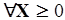 ,
,
F = - 2X2 + X4 + 3X5  max.
max.
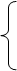 14. X1 + 4X2 + X3 = 2,
14. X1 + 4X2 + X3 = 2,
X1 + 2X2 - X3 = 0,
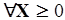 ,
,
F = X1 + 10X2 + 8X3  max.
max.
Обработка результатов эксперимента производится во многих технических расчетах с целью решения одной из следующих задач:
1. Аппроксимации – экспериментальные точки надо соединить плавной кривой и подобрать ее функциональное выражение (рис. 2.1,а).
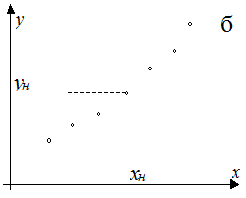
2. Интерполяции – на основе обработки экспериментальных данных требуется найти координату какой-либо неизвестной точки (x, y) на данном интервале, в пределах диапазона измеряемой величины (рис. 2.1,б).
3. Экстраполяции – на основе обработки экспериментальных данных требуется найти координату какой-либо неизвестной точки (x, y) за пределами диапазона измеряемой величины (рис. 2.1,в).
Во всех трех задачах требуется найти функциональную зависимость (уравнение), которая представляет результаты эксперимента.
|
|
|
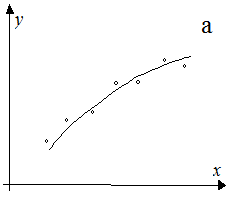
Уравнение, представляющее результаты эксперимента, но которое нельзя найти только теоретическим путем, называют эмпирическим уравнением или эмпирической формулой. Таким образом, прежде всего следует установить общий вид эмпирической формулы, а затем находить ее коэффициенты.
Идеальная эмпирическая формула должна достаточно точно представлять опытные данные и одновременно быть достаточно простой, то есть иметь как можно меньше коэффициентов. Кроме того, в ряде технических задач, по характеру наблюдаемого процесса, может быть отдельно оговорено, какой функцией (линейной, гиперболической, квадратичной и т.д.) следует сглаживать результаты опыта.
Выбрав тип уравнения, необходимо определить его коэффициенты. Линия должна проходить как можно ближе ко всем данным точкам и отклонения должны быть с обоими знаками, т.е. положительные и отрицательные. Наиболее вероятные значения коэффициентов определяются по методу наименьших квадратов (МНК). Поскольку данный метод требует большого количества вычислений, то расчеты целесообразно производить на ЭВМ.
Основная идея МНК заключается в следующем. Пусть результаты измерений представлены значениями:
| X | x1 | x2 | … | xn |
| Y | y1 | y2 | … | yn |
И пусть y = j(x) - искомая эмпирическая формула.
 Требуется так подобрать параметры функции j(x), чтобы разности j(xi) – yi (i= 1, n) были наименьшими. Так как разности могут быть как положительными, так и отрицательными (рис. 2.2), то за критерий качества аппроксимации принимают наименьшую сумму квадратов разностей:
Требуется так подобрать параметры функции j(x), чтобы разности j(xi) – yi (i= 1, n) были наименьшими. Так как разности могут быть как положительными, так и отрицательными (рис. 2.2), то за критерий качества аппроксимации принимают наименьшую сумму квадратов разностей:
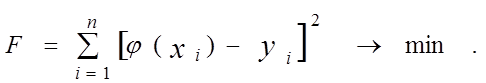 (2.1)
(2.1)
Рассмотрим наиболее часто встречающиеся на практике случаи, когда функция j(x):
1). линейная;
2). квадратическая (парабола);
3). гиперболическая.
|
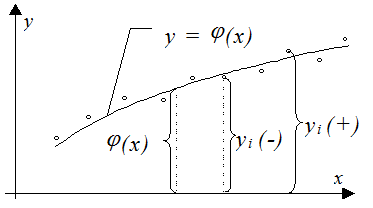
Аппроксимация линейной функцией
 Пусть из опыта получена следующая совокупность значений xi и yi: i= 1, n. Требуется подобрать по МНК параметры a0 и a1 линейной функции y = a0 x + a1 , изображающей данную экспериментальную зависимость. Найдем значения a0 и a1 , при которых достигается минимум суммы квадратов отклонений.
Пусть из опыта получена следующая совокупность значений xi и yi: i= 1, n. Требуется подобрать по МНК параметры a0 и a1 линейной функции y = a0 x + a1 , изображающей данную экспериментальную зависимость. Найдем значения a0 и a1 , при которых достигается минимум суммы квадратов отклонений.
Для этого продифференцируем функцию j(x) по a0 и a1 (2.1) и приравняем производные к нулю, получим:
2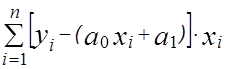 = 0, где
= 0, где 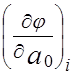 =
= 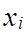 ;
;
2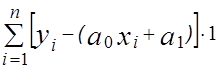 = 0, где
= 0, где 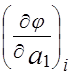 = 1.
= 1.
Преобразуя полученные уравнения, находим:
|
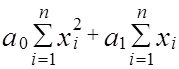 =
= 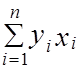 ,
,
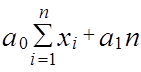 =
= 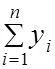 .
.
Нормальная система (2.2) всегда имеет единственное решение (a0 , a1), которое можно найти по формулам Крамера или методом исключения переменных.
|
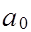 =
= 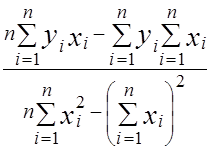 ,
,
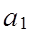 =
= 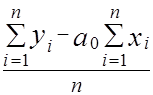 .
.
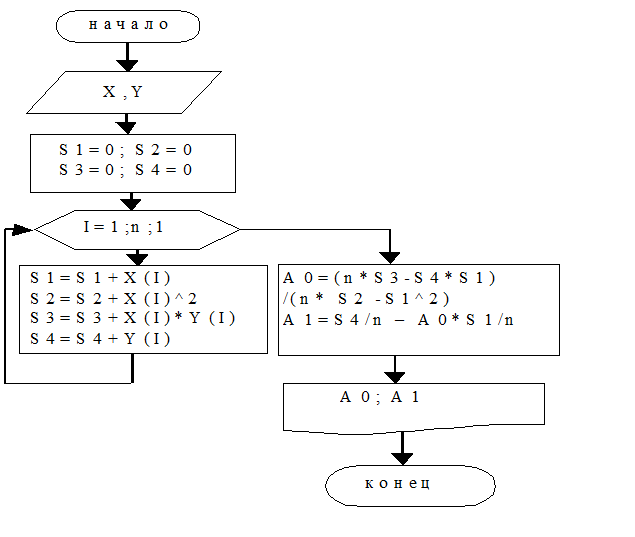
Алгоритм вычислительного процесса для аппроксимации результатов наблюдений линейной эмпирической формулой показан на рис. 2.3, где
S1 = 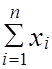 ; S2 =
; S2 = 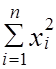 ; S3 =
; S3 = 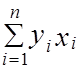 ; S4 =
; S4 = 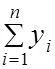 .
.
|
Аппроксимация квадратичной функцией.
Требуется с помощью МНК подобрать параметры уравнения
y = a0 x2 +a1 x + a2,
соответствующего наблюдаемой экспериментальной зависимости.
Имеем j(x) = a0 x2 +a1 x + a2;
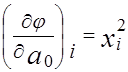 ;
; 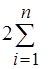 [ y i - (a 0 x
[ y i - (a 0 x + a1 x i + a2 ) ]
+ a1 x i + a2 ) ]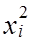 =0;
=0;
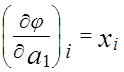 ;
; 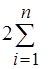 [ y i - (a 0 x
[ y i - (a 0 x + a1 x i + a2 ) ] x i =0;
+ a1 x i + a2 ) ] x i =0;
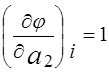 ;
; 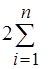 [ y i - (a 0 x
[ y i - (a 0 x + a1 x i + a2 ) ] 1 =0.
+ a1 x i + a2 ) ] 1 =0.
Приведем полученные уравнения к нормальному виду:
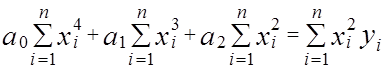 ,
,
|
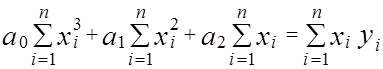 ,
,
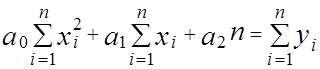 .
.
Решая систему (2.4), например методом Гаусса, находим значения a0 , a1 ,a2 .
 2014-02-09
2014-02-09 669
669