Аппроксимация функциональной зависимостью вида. Аппроксимация гиперболической функцией

Аппроксимация гиперболической функцией

Требуется с помощью МНК подобрать параметры уравнения

y =a₀ + a₁ /x,

соответствующего наблюдаемой экспериментальной зависимости.

Имеем: j(x) =a₀ + a₁ /x,

2 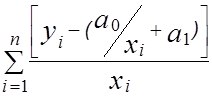=0, где = ;

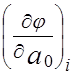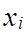2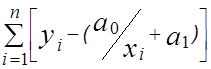= 0, где 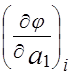= 1.

Тогда

=

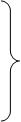
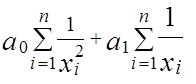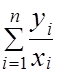
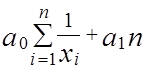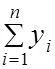
Из полученной системы (2.5) находим a₀ и a₁.

y = a₀ exp(a₁ x) (2.6)

Прологарифмировав (2.6), получим ln y = ln a₀ + a₁ x

Введя обозначения ln y = Y и ln a₀ = A₀, получим следующую зависимость: Y= a₁ x + A₀,

т.е. линейную функцию переменной x с параметрами a₁ и A₀ .

Имея результаты опыта в виде n пар

перейдем к парам

где Y _i = ln y_i, а затем для этой линейной зависимости определим приближенно параметры a ₁ и A₀ по формуле (2.3).