ГРУППОВЫЕ КОДЫ И СПОСОБЫ ИХ ОПИСАНИЯ
Задачи
1. Определить долю необнаруживаемых трансформаций кодовых комбинаций при передаче информации по каналу с помехами обнаруживающим ошибки кодом, имеющим длину кодовой комбинации n = 256 и число избыточных элементов 16.
2. Определить возможности кода Голея, имеющего n =23, k = 12, dmin = 7 по исправлению, обнаружению, а также совместному обнаружению и исправлению ошибок.
3. Для передачи информации с исправлением однократных ошибок применен код, состоящий из двух комбинаций: 001 и 110. Определить состав защитных зон этих комбинаций.
4. Выбран код, состоящий из следующих четырех комбинаций
11010, 01101, 10111, 00001.
Какую из кодовых комбинаций следует заменить на чисто нулевую комбинацию (00000), чтобы код имел dmin =3?
Современные и перспективные помехоустойчивые коды строятся на основе некоторой математической модели, что позволяет достаточно просто решать вопросы определения их свойств и реализуемости. При построении кодов используются алгебраические системы: группа, векторное пространство, кольцо и поле.
а) Группа
Пусть имеется множество G элементов произвольной природы, которые обозначим a, b, c…, и пусть над этими элементами можно производить операцию сложения или умножения таким образом, что двум любым элементам множества G по определенным правилам ставится в однозначное соответствие некоторый элемент того же множества G. В общем виде введенную операцию будем обозначать знаком  . Для операции сложения и умножения будем использовать общепринятые знаки (“+” и ”
. Для операции сложения и умножения будем использовать общепринятые знаки (“+” и ” ” соответственно).
” соответственно).
Множество G называют группой, если для введенной операции оно удовлетворяет следующим требованиям:
G1. Множество замкнуто: если a и b принадлежат G, то и c, полученное на основе введенной операции 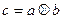 также принадлежит этому же множеству элементов G. При сложении
также принадлежит этому же множеству элементов G. При сложении 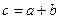 , при умножении
, при умножении 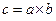 .
.
G2. Выполняется сочетательный (ассоциативный) закон:
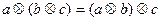 .
.
При сложении 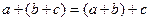 ,
,
При умножении 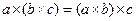 .
.
G3. Наличие единичного элемента e: среди элементов множества G имеется такой элемент e, для которого справедливо 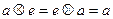 , где a - произвольный элемент G.
, где a - произвольный элемент G.
В случае операции сложения над числами равенство 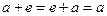 возможно лишь в том случае, когда e = 0. Если же над числами производится операция умножения, то равенство
возможно лишь в том случае, когда e = 0. Если же над числами производится операция умножения, то равенство 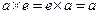 возможно лишь в том случае, когда e = 1.
возможно лишь в том случае, когда e = 1.
G4. Наличие обратных элементов: для произвольного элемента а множества G существует в этом множестве такой элемент 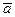 , для которого справедливо
, для которого справедливо
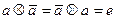 .
.
Если элементами множества G являются числа, то при сложении 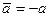 , а при умножении
, а при умножении 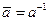 .
.
Примеры групп:
1. Множество целых чисел положительных, отрицательных и нуля является группой по операции сложения.
2. Числа 0 и 1 образуют группу по операции “сложение по модулю 2”.
1) Замкнутость. Обусловлена таблицей сложения
| + | ||
2) Сочетательность. Легко проверить, что сложение по модулю 2 подчиняется сочетательному закону, например
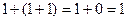 ,
,
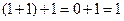 .
.
3) Единичный элемент. Здесь 0 является единичным элементом
4) Обратные элементы. Каждое число является обратным к самому себе, т.к. 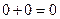 и
и 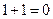 .
.
Пример 5.1. Проверить, является ли множество трехразрядных комбинаций 000,001, 010 и 011 группой по операции поразрядного сложения по модулю 2.
1) Замкнутость. Составим таблицу сложения:
| + |  |  |  |  |
Мы видим, что сумма любой пары комбинаций также является комбинацией из данного множества, т.е. требование замкнутости удовлетворяется.
2) Сочетательность. Это требование также удовлетворяется, т.к. в основе операции – сложение по модулю 2.
3) Единичный элемент. Комбинация 000 является единичным элементом в данном множестве (см. таблицу сложения).
4) Обратные элементы. Обратной комбинацией для любой комбинации является эта же комбинация (см. таблицу сложения).
Итак, множество комбинаций 000, 001, 010 и 011 является группой по операции поразрядного сложения по модулю 2.
Группа называется абелевой в честь известного норвежского математика Н.Х. Абеля (1802-1829), если множество G по введенной операции обладает еще и следующими свойствами: 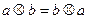 , т.е. выполняется переместительный (коммутативный) закон. Группы, рассмотренные в предыдущих примерах, являются абелевыми.
, т.е. выполняется переместительный (коммутативный) закон. Группы, рассмотренные в предыдущих примерах, являются абелевыми.
Важным понятием в теории групп является понятие подгруппы.
Если множество элементов 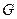 составляет группу и некоторая часть этого множества (Н) также обладает всеми групповыми свойствами, то эту часть элементов группы называют подгруппой. Слово “подгруппа” означает “группа внутри группы”. Для того, чтобы установить, является ли Н подгруппой
составляет группу и некоторая часть этого множества (Н) также обладает всеми групповыми свойствами, то эту часть элементов группы называют подгруппой. Слово “подгруппа” означает “группа внутри группы”. Для того, чтобы установить, является ли Н подгруппой 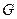 необходимо проверить замкнутость и наличие обратных элементов. Если множество Н замкнуто относительно заданной в группе операций и содержит обратные элементы, то это множество содержит и единичный элемент группы, а сочетательный закон выполняется, так как он справедлив для всех элементов группы.
необходимо проверить замкнутость и наличие обратных элементов. Если множество Н замкнуто относительно заданной в группе операций и содержит обратные элементы, то это множество содержит и единичный элемент группы, а сочетательный закон выполняется, так как он справедлив для всех элементов группы.
Основные свойства группы:
1. Группа содержит единственный единичный элемент, и для каждого элемента группы имеется единственный обратный элемент.
2. Группа разлагается на смежные классы по подгруппе. Смысл этого разложения заключается в следующем.
Обозначим элемент группы 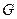 через
через 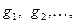 а элемент подгруппы Н – через
а элемент подгруппы Н – через 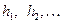 Рассмотрим таблицу, образованную следующим образом.
Рассмотрим таблицу, образованную следующим образом.
Запишем все элементы подгруппы Н, начиная с единичного элемента, в первую строку, причем каждый элемент подгруппы появится в этой строке только один раз. Далее выбираем любой элемент 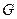 , не принадлежащий Н, и записываем его на первое место во второй строке, а все остальные элементы второй строки находятся применением заданной в группе операции над первым элементом второй строки и соответствующими элементами подгруппы H, записанными в первой строке. Аналогично образуются третья, четвертая и т.д. строки, до тех пор, пока все элементы
, не принадлежащий Н, и записываем его на первое место во второй строке, а все остальные элементы второй строки находятся применением заданной в группе операции над первым элементом второй строки и соответствующими элементами подгруппы H, записанными в первой строке. Аналогично образуются третья, четвертая и т.д. строки, до тех пор, пока все элементы  не войдут в таблицу. В качестве первого элемента каждой строки всякий раз выбирается произвольный элемент
не войдут в таблицу. В качестве первого элемента каждой строки всякий раз выбирается произвольный элемент  , не вошедший в предшествующие строки. Этот элемент называют образующим смежного класса.
, не вошедший в предшествующие строки. Этот элемент называют образующим смежного класса.
В результате получаем таблицу следующего вида:
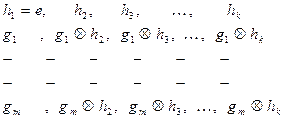
Строки полученной подобным образом таблицы называются смежными классами.
Основные свойства разложения группы на смежные классы по подгруппе формулируются следующим образом:
3. В таблице разложения группы  на смежные классы по подгруппе Н перечисляются все элементы группы
на смежные классы по подгруппе Н перечисляются все элементы группы  , причем каждый элемент появляется в таблице только один раз.
, причем каждый элемент появляется в таблице только один раз.
4. Состав смежного класса постоянен и не зависит от выбора образующего элемента.
5. Число элементов в Н является делителем числа элементов в 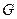 .
.
6. Два элемента gi и gj группы G принадлежит одному и тому смежному классу по подгруппе H тогда и только тогда, когда gi 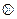 gj принадлежат H.
gj принадлежат H.
7. Операция, введенная над элементами группы, может быть введена и над смежными классами. Обозначим{ gi } смежный класс, содержащий элемент группы {gi}. Тогда {gi}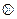 { gj }={ gi
{ gj }={ gi 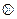 gj }, т.е. в результате операции над смежными классами, содержащими элементы gi и gj, получается новый смежный класс, содержащий gi
gj }, т.е. в результате операции над смежными классами, содержащими элементы gi и gj, получается новый смежный класс, содержащий gi 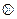 gj. В случае абелевой группы операция над смежными классами приводит к группе, элементами, которой является смежные классы.
gj. В случае абелевой группы операция над смежными классами приводит к группе, элементами, которой является смежные классы.
Пример 5.2.
Пусть G - группа по операции сложения (т.е. аддитивная группа), состоящая из всех положительных и отрицательных целых чисел и нуля, и пусть H – подгруппа, состоящая из всех чисел, кратных целому числу n. Все числа от нуля до n -1 принадлежат различным смежным классам, т.к. для того, чтобы a и b принадлежали одному смежному классу необходимо, чтобы число (-a)+b принадлежало подгруппе, т.е. было кратно n, что невозможно. Значит, числа от 0 до n -1 могут быть выбраны в качестве образующих смежных классов и других чисел, быть не может. Легко проверить, что группа G - абелева, поэтому можно ввести операцию сложения смежных классов и смежные классы образуют группу. Положим n=2. Тогда смежные классы имеют вид:
0, 2, -2, 4, -4, 6, -6,…
1, 3, -1, 5, -3, 7, -5,…
Если обозначить смежные классы {0}и {1} соответственно, то таблица сложения смежных классов получит вид:
| + | {0} | {1} |
| {0} | {0} | {1} |
| {1} | {1} | {0} |
В этой таблице легко узнается таблица сложения чисел по модулю 2.
Множество элементов произвольной природы V, называемых далее векторами, образует векторное пространство, если оно удовлетворяет следующим требованиям.
1. Множество векторов образует абелеву группу по операции сложения векторов.
2. Определено правило умножения вектора 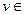 V на скаляр с, где с в рассматриваемом нами случае принимает значение 0 или 1, и произведение
V на скаляр с, где с в рассматриваемом нами случае принимает значение 0 или 1, и произведение 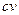 является вектором того же векторного пространства V.
является вектором того же векторного пространства V.
3. Выполняется распределительный закон:
- если с и d скаляры, а v - вектор (v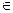 V), то
V), то 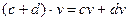 ,
,
- если v и u – векторы (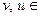 V), а с – скаляр, то
V), а с – скаляр, то 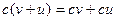 .
.
4. Операция умножения на скаляр подчиняется сочетательному закону: если с, d – скаляры, а v - вектор (v 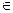 V), то
V), то 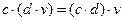 .
.
Пример 5.3. Проверить, является ли набор комбинаций 000,001,010 и 011 векторным пространством.
В примере 5.1. было показано, что эти комбинации образуют группу по операции поразрядного сложения по модулю 2. Так как для любых комбинаций порядок сложения не существенен, например,001+010=010+001=011, то эта группа является абелевой.
Будем полагать каждую комбинацию вектором и умножение на скаляр производить следующим образом: 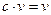 , если с = 1, и
, если с = 1, и 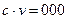 , если с = 0, где v - любая из рассматриваемых комбинаций.
, если с = 0, где v - любая из рассматриваемых комбинаций.
При таком введении операции умножения на скаляр выполняются распределительные законы, например
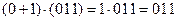
или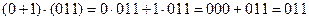
и 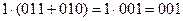
или 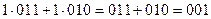
Операция умножения на скаляр подчиняется сочетательному закону, например,
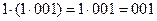 или
или 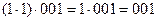 .
.
Таким образом, набор комбинаций 000, 001, 010 и 011 при введении операций указанным выше способом удовлетворяет требованиям векторного пространства.
Рассмотренный пример показывает, что для двоичного случая свойства векторного пространства в основном определены свойствами абелевой группы.
Сформулируем некоторые понятия и определения, относящиеся к векторному пространству.
1) Сложение векторов
Пусть V и 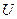 - два вектора n – мерного векторного пространства
- два вектора n – мерного векторного пространства 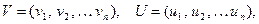 где
где 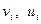 - скаляры (двоичные элементы). Тогда суммой этих векторов будем называть новый вектор
- скаляры (двоичные элементы). Тогда суммой этих векторов будем называть новый вектор 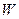 , образованный по следующему правилу:
, образованный по следующему правилу:
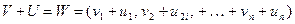 .
.
2) Умножение вектора на скаляр
Пусть 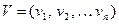 вектор, а с – скаляр. Умножение вектора на скаляр дает новые вектор, образованный по следующему правилу:
вектор, а с – скаляр. Умножение вектора на скаляр дает новые вектор, образованный по следующему правилу:
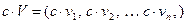 .
.
3) Скалярное произведение векторов
Пусть V и U векторы: 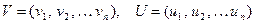 . Скалярным произведением векторов называется скаляр (двоичный элемент), образованный по следующему правилу:
. Скалярным произведением векторов называется скаляр (двоичный элемент), образованный по следующему правилу:
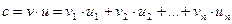
Знак “+”здесь имеет смысл сложения по модулю 2.
Если скалярное произведение векторов равно 0, то такие векторы называются ортогональными.
4) Линейная комбинация векторов
Линейной комбинацией векторов 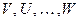 называют вектор
называют вектор 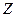 , образованный по следующему правилу:
, образованный по следующему правилу:
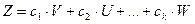 , где
, где 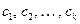 - скаляры (двоичные элементы).
- скаляры (двоичные элементы).
5) Линейная зависимость векторов
Если 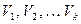 есть векторы,
есть векторы, 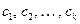 есть скаляры, причем хотя бы один из них не равен0, то указанный набор векторов называется линейно-зависимым, если
есть скаляры, причем хотя бы один из них не равен0, то указанный набор векторов называется линейно-зависимым, если
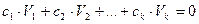
В этом случае, когда эта сумма обращается в 0 (чисто нулевой вектор 00…0) только лишь при равенстве всех скаляров нулю, этот набор векторов называют линейно-независимым.
6) Базис векторного пространства
Векторное пространство размерности n (n – мерное векторное пространство) со значением скаляров 0 или 1 содержит в своем составе 2 n различных векторов.
Это пространство может быть охарактеризовано базисом, состоящим из n линейно независимых векторов. Все остальные векторы можно получить путем линейных комбинаций базисных векторов.
Подпространство n – мерного векторного пространства размерности k, где k<n, содержит 2 k различных векторов, выбранных на 2 n векторов, составляющих n – мерное пространство, таким образом, что удовлетворяются все требования векторного пространства. Любой набор из k линейно-независимых векторов данного пространства может служить его базисом.
Пример 5.4. Набор векторов 000, 001, 010, 011, 100, 101, 110, 111 образует 3-мерное векторное пространство (23 векторов). Его базисом могут служить следующие тройки векторов:
001, 010, 100 или 010, 011, 110 и т.д.
С помощью базисных векторов можно получить любой другой вектор данного 3-мерного пространства. Используя линейную комбинацию базисных векторов
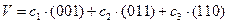 ,
,
получим, например, вектор101. Для этого надо взять 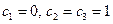 , тогда
, тогда

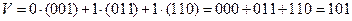 .
.
Подбором 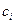 можно получить каждый вектор рассматриваемого пространства.
можно получить каждый вектор рассматриваемого пространства.
В примере 5.3. мы установили, что набор векторов 000, 001, 010 и 011 удовлетворяет всем требованиям векторного пространства.
По отношению к полному набору векторов 3-мерного векторного пространства данный набор векторов является подпространством размерности 2.
Его базисы 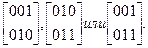
 2014-02-13
2014-02-13 952
952