Групповым кодом называю такой код, множество кодовых комбинаций которого образует группу (подгруппу) по операции поразрядного сложения по модулю 2
Если в кодовой комбинации группового кода известны места информационных и избыточных элементов, то такой групповой код называют систематическим. В систематических кодах введение избыточности в кодовые комбинации осуществляется на основе связи между информационными и избыточными элементами. Название “систематический” коду дано вследствие того, что связь между информационными и избыточными элементами задается в виде систем линейных соотношений. Итак, систематический код – это разделимый групповой код. Групповая структура кода обеспечивает ему ряд важных свойств.
Свойство 5.1. Минимальное кодовое расстояние группового кода равно минимальному весу его ненулевых кодовых комбинаций.
Действительно, кодовое расстояние между комбинациями определяется как вес суммы двух комбинаций. В силу свойства замкнутости сумма двух комбинаций также является кодовой комбинацией, т.к. таблице кодовых расстояний группового кода однозначно соответствует таблица весов кодовых комбинаций данного кода, а раз так, то и минимальному кодовому расстоянию в групповом коде соответствует ненулевая кодовая комбинация с минимальным весом.
Другие важные свойства, обусловленные групповой структурой кодов, будут изучены в связи с матричным описанием этих кодов.
Для групповых кодов существует специальное обозначение (n, k) – код, где n - длина кодовой комбинации, k - число информационных элементов.
5.2.4 Матричное описание групповых кодов
Отождествление кодовых комбинаций групповых кодов с векторами позволяет упростить их задание и описание.
Известно, что векторное пространство однозначно определяется своим базисом. Поэтому естественно стремление использовать базис векторного пространства для описания (n, k) – кода, соответствующего данному векторному пространству. Используя понятие базиса, можно утверждать, что для описания (n, k) – кода достаточно использовать k линейно независимых кодовых комбинаций, т.е. справедливо следующее:
Свойство 5.2. Групповой (n, k) – код полностью определяется набором из k линейно независимых комбинаций, принадлежащих этому коду.
Обычно эти k линейно независимые комбинации записывают в виде прямоугольной таблицы - матрицы, имеющей k строк и n столбцов, где строками являются кодовые комбинации.
По аналогии с векторным пространством все остальные кодовые комбинации могут быть получены путем линейной комбинации строк построенной матрицы. В связи с этим указанную прямоугольную матрицу принято называть порождающей матрицей группового кода.
Для порождающей матрицы будем использовать обозначение G ( n, k ). Размерность порождающей матрицы (k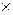 n).
n).
Пример 5.5. Построим (5, 3) – код. Такой код должен иметь 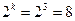 кодовых комбинаций. В качестве информационной части используем всевозможные двоичные последовательности длины три. Условимся первые два разряда в кодовой комбинации
кодовых комбинаций. В качестве информационной части используем всевозможные двоичные последовательности длины три. Условимся первые два разряда в кодовой комбинации 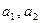 отводить под избыточные элементы; а три последние
отводить под избыточные элементы; а три последние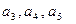 под информационные. Пусть проверочные элементы формируются как сумма по модулю 2 определенных информационных элементов:
под информационные. Пусть проверочные элементы формируются как сумма по модулю 2 определенных информационных элементов: 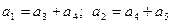 .
.
Используя такой принцип построения кодовой комбинации (5, 3) – кода, получаем все его комбинации в следующем виде:
| Простой код | (5, 3) –код | Вес кодовой комбинации | |
Анализируя веса кодовых комбинаций, приходим к выводу, что минимальное кодовое расстояние в данном коде равно 2.
В этом можно убедиться, построив таблицу кодовых расстояний для данного кода:
Можно указать несколько троек линейно-независимых комбинаций этого кода. Например:
4. 10100 4. 10100 4. 10100
2. 11010 5. 11101 6. 01110
1. 01001 6. 01110 7. 00111
и так далее.
Каждый из этих наборов комбинаций может служить порождающей матрицей данного (5, 3) – кода.
Предположим, что в качестве порождающей матрицы данного кода (5, 3) выбраны кодовые комбинации
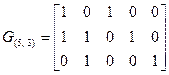
Покажем, что все кодовые комбинации могут быть получены как линейные комбинации базисных векторов, т.е. строк порождающей матрицы:
00000=0(10100)+0(11010)+0(01001),
01001=0(10100)+0(11010)+1(01001),
11010=0(10100)+1(11010)+0(01001),
10011=0(10100)+1(11010)+1(01001),
10100=1(10100)+0(11010)+0(01001),
11101=1(10100)+0(11010)+1(01001),
01110=1(10100)+1(11010)+0(01001),
00111=1(10100)+1(11010)+1(01001).
Аналогично можно показать, что любой другой набор линейно-независимых комбинаций порождает тот же самый код.
Преимущество матричного описания кодов очевидно по сравнению с перечислением всех кодовых комбинаций. Действительно, если (n, k) – код содержит 2 k комбинаций, то для его задания требуется всего лишь k кодовых комбинаций.
Представляет интерес определить число возможных порождающих матриц для групповых кодов с параметрами n и k. Для этого подсчитаем сколькими способами можно набрать k линейно независимых строк порождающей матрицы из 2 k – 1 кодовых комбинаций (чисто нулевая кодовая комбинация, естественно, исключается). В качестве первой строки может быть выбрана любая из 2 k – 1 кодовых комбинаций (т.е. 2 k – 1 способов). Так как среди кодовых комбинаций нет повторяющихся, то в качестве второй строки можно выбрать любую их оставшихся 2 k – 2 комбинаций (2 k – 2 способов). При выборе третьей строки следует исключить из рассмотренных, кроме двух записанных строк, их сумму, т.е. третья строка может быть выбрана 2 k – 22 способами. Рассуждая аналогично, находим, что при выборе i – той строки следует исключить из рассмотрения все линейные комбинации (i - 1) предшествующих строк, т.е. 2 i – 1 комбинаций.
Общее же число наборов k линейно независимых комбинаций из множества 2 k кодовых комбинаций составит число
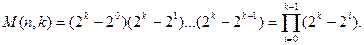
Для группового кода (5,3) полное число возможных порождающих матриц оказывается равным
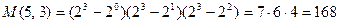
Столь большое число возможных порождающих матриц для (n, k) - кода затрудняет их использование для задания кода.
Для однозначности задания кода порождающей матрицей вводят понятие о канонической форме порождающей матрицы.
Каноническая форма порождающей матрицы имеет следующий вид:
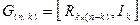 ,
,
где Ik – единичная матрица размерности (k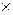 k), то есть такая квадратная матрица, у которой на главной диагонали находятся единицы, а все остальные элементы – нули. Ik содержит информационные элементы кодовых комбинаций, образующих порождающую матрицу.
k), то есть такая квадратная матрица, у которой на главной диагонали находятся единицы, а все остальные элементы – нули. Ik содержит информационные элементы кодовых комбинаций, образующих порождающую матрицу. 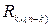 - матрица размерности
- матрица размерности 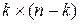 , составленная из проверочных элементов базисных кодовых комбинаций.
, составленная из проверочных элементов базисных кодовых комбинаций.
Для рассмотренного выше кода (5, 3) каноническая форма порождающей матрицы имеет вид:
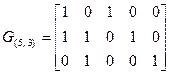
В линейной комбинации строк порождающей матрицы примера 5.5. скаляры при строках в своей совокупности повторяют информационную часть отыскиваемой кодовой комбинации. Из этого вытекает важный вывод: для получения кодовой комбинации (n,k)-кода по ее информационной части необходимо умножить последовательность длины k, являющейся информационной частью кодовой комбинации, на порождающую матрицу этого кода в канонической форме по правилам умножения матриц:
(k- последовательность)×G(n,k)=[комбинация (n,k)-кода].
Матрица 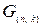 может быть преобразована к канонической форме при любом исходном наборе базисных кодовых комбинаций посредством элементарных операций над строками матрицы, которые включают:
может быть преобразована к канонической форме при любом исходном наборе базисных кодовых комбинаций посредством элементарных операций над строками матрицы, которые включают:
1) перестановку любых двух строк;
2) умножение любой строки на скаляр;
3) прибавление произведения одной из строк матрицы на скаляр к другой строке матрицы;
Порождающая матрица (n, k) – кода в канонической форме задает тот же самый код, что и исходная порождающая матрица, т.к. пространства строк этих матриц совпадают в силу выполнения свойства замкнутости.
Пример5.6. Рассмотрим процедуру приведения матрицы G (5, 3) кода предыдущего примера к канонической форме.
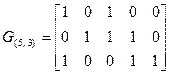
Первая строка матрицы соответствует канонической форме, а вторая и третья должны быть преобразованы. Прибавим ко второй строке первую и результат запишем во второй строке матрицы:
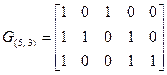
Затем прибавим к третьей строке вторую, а результат запишем в третьей строке
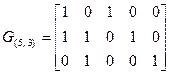
Итак, каноническая форма матрицы кода (5, 3) имеет уже известный вид.
Следует отметить, что если элементарные операции над строками порождающей матрицы в результате дают в точности тот же самый код, то применение элементарных операций к столбцам матрицы приводит к новому коду, корректирующие свойства которого могут отличаться от свойств исходного кода. Только лишь перестановка столбцов не изменяет весов кодовых комбинаций, а в некоторых случаях и их вида. Поэтому (n, k) – коды, полученные из матрицы 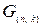 некоторого (n, k) – кода перестановкой столбцов этой матрицы, называют эквивалентными. Таким образом, перестановка столбцов порождающей матрицы (n, k) – кода дает порождающую матрицу для эквивалентного кода (n, k) – кода.
некоторого (n, k) – кода перестановкой столбцов этой матрицы, называют эквивалентными. Таким образом, перестановка столбцов порождающей матрицы (n, k) – кода дает порождающую матрицу для эквивалентного кода (n, k) – кода.
Заметим, что единичная матрица Ik в канонической форме порождающей матрицы может находиться либо перед матрицей 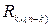 проверочных элементов, либо после нее в зависимости от того, где в кодовой комбинации располагаются информационные элементы – в начале или конце комбинации. Понятие об эквивалентности кодов позволяет находить каноническую форму порождающей матрицы неразделимого группового кода.
проверочных элементов, либо после нее в зависимости от того, где в кодовой комбинации располагаются информационные элементы – в начале или конце комбинации. Понятие об эквивалентности кодов позволяет находить каноническую форму порождающей матрицы неразделимого группового кода.
Широкое применение нашел также и другой способ матричного описания кодов. Сущность его сводится к следующему. Если записать правило формирования каждого их проверочных соотношений кодовой комбинации в виде вектора из нулей и единиц, где единицы указывают, какие элементы кодовой комбинации охвачены проверкой на четность, то получим n - k векторов. Такие векторы получили название проверочных. Так как каждый проверочный вектор отражает проверку на четность, введенную для любой кодовой комбинации, то справедливо следующее.
Свойство 5.3. Скалярное произведение любой кодовой комбинации на проверочный вектор равно нулю.
Действительно, обозначим проверочный вектор через 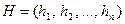 , а кодовую комбинацию через
, а кодовую комбинацию через 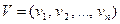 , тогда их скалярное произведение равно
, тогда их скалярное произведение равно 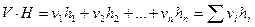 . Сумма берется по всем слагаемым, в которых
. Сумма берется по всем слагаемым, в которых 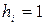 , т.е. сводится к сумме элементов кодовой комбинации, охваченных проверкой на четность, а потому эта сумма должны дать 0. Записывая проверочные вектора в прямоугольную таблицу, получим проверочную матрицу кода, обозначаемую H(n, k) и имеющую размерность
, т.е. сводится к сумме элементов кодовой комбинации, охваченных проверкой на четность, а потому эта сумма должны дать 0. Записывая проверочные вектора в прямоугольную таблицу, получим проверочную матрицу кода, обозначаемую H(n, k) и имеющую размерность 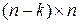 . Единицы на позициях, соответствующих информационным элементам в кодовой комбинации, указывают, какие информационные элементы участвуют в формировании проверочного элемента, а единица на позициях избыточных элементов указывает, какой именно проверочный элемент образован данной суммой информационных элементов Так как каждый полученный таким образом проверочный вектор отличается от других, по крайней мере, видом элементов, соответствующих избыточным разрядам, то все (n-k) проверочных вектора являются линейно независимыми. Это означает, что матрица H(n, k) является базисом подпространства n – мерного векторного пространства размерности (n-k), каждый вектор которого ортогонален любой кодовой комбинации. Такое подпространство называют нулевым пространством кода или двойственным кодом.
. Единицы на позициях, соответствующих информационным элементам в кодовой комбинации, указывают, какие информационные элементы участвуют в формировании проверочного элемента, а единица на позициях избыточных элементов указывает, какой именно проверочный элемент образован данной суммой информационных элементов Так как каждый полученный таким образом проверочный вектор отличается от других, по крайней мере, видом элементов, соответствующих избыточным разрядам, то все (n-k) проверочных вектора являются линейно независимыми. Это означает, что матрица H(n, k) является базисом подпространства n – мерного векторного пространства размерности (n-k), каждый вектор которого ортогонален любой кодовой комбинации. Такое подпространство называют нулевым пространством кода или двойственным кодом.
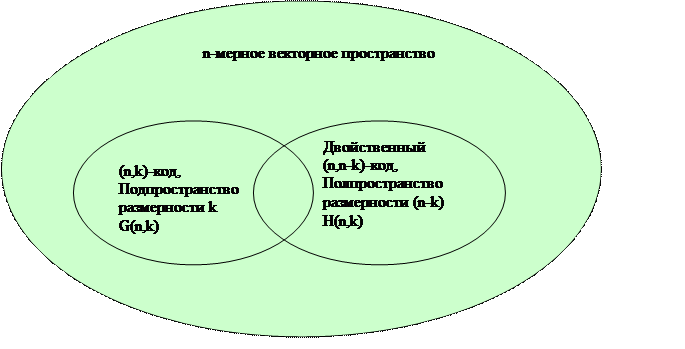 Рис5.5
Рис5.5
Векторные подпространства построенные на основе порождающей G(n,k) и проверочной H(n,k) матриц
Проверочная матрица позволяет формализовать процесс вычисления проверочных соотношений для любой кодовой комбинации, сведя его к произведению кодовой комбинации на проверочную матрицу по правилам умножения матриц: 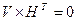 , то есть некоторая комбинация V принадлежит (n, k) – коду тогда и только тогда, когда она ортогональна каждой строке матрицы H(n, k). Соотношение
, то есть некоторая комбинация V принадлежит (n, k) – коду тогда и только тогда, когда она ортогональна каждой строке матрицы H(n, k). Соотношение 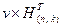 лежит в основе процедуры декодирования для групповых кодов.
лежит в основе процедуры декодирования для групповых кодов.
В результате умножения принятой комбинации на матрицу проверок получаем вектор из (n-k) символов, называемый синдромом. В случае, если синдром чисто нулевой, то кодовая комбинация считается принятой безошибочно. При наличии в синдроме ненулевых компонент фиксируется наличие ошибок в кодовой комбинации.
Пример 5.7. Для рассматриваемого выше группового (5, 3) - кода проверочные вектора имеют вид:
1 0 1 1 0 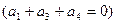 ,
,
0 1 0 1 1 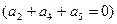 .
.
Проверочная матрица:
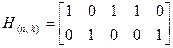
Двойственный код содержит 4 комбинации:
1 0 1 1 0
0 1 0 1 1
1 1 1 0 1
0 0 0 0 0
Это (5,2) – код с dmin=3
Каноническая форма матрицы H(n, k) имеет следующий вид:
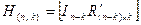 ,
,
где In-k – единичная матрица размеров 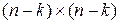 занимает места, соответствующие избыточным элементам кодовой комбинации;
занимает места, соответствующие избыточным элементам кодовой комбинации;
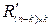 - матрица размеров
- матрица размеров 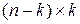 , расположенная на местах, соответствующих информационным элементам; каждая строка этой матрицы указывает, какие информационные элементы кодовой комбинации охвачены проверками на четность.
, расположенная на местах, соответствующих информационным элементам; каждая строка этой матрицы указывает, какие информационные элементы кодовой комбинации охвачены проверками на четность.
Вид матрицы 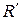 устанавливается на основе следующего свойства.
устанавливается на основе следующего свойства.
Свойство 5.4. Если 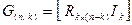 есть порождающая матрица систематического (n, k) – кода в канонической форме, то нулевое пространство этого кода порождается матрицей
есть порождающая матрица систематического (n, k) – кода в канонической форме, то нулевое пространство этого кода порождается матрицей 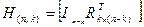 .
.
Доказательство этого свойства основывается на следующих рассуждениях. Поскольку любая кодовая комбинация при умножении на транспонированную проверочную матрицу должна давать (n-k) – разрядный нулевой вектор, то этот же результат должен быть получен при умножении каждой строки порождающей матрицы на проверочную матрицу, а, следовательно, и умножение матрицы 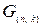 на матрицу
на матрицу 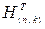 дает нулевую матрицу размеров
дает нулевую матрицу размеров 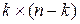 , т.е. справедливо равенство
, т.е. справедливо равенство 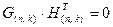 .
.
Решение данного матричного уравнения и позволяет установить вид проверочной матрицы:
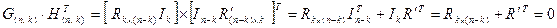 ,
,
т.е. 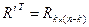 или R'=
или R'=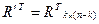 .
.
Итак, порождающая матрица (n, k) – кода является сокращенной записью кода. Проверочная матрица указывает соотношение между избыточными и информационными элементами в каждой кодовой комбинации. Между порождающей и проверочной матрицами в канонической форме существует жесткая связь, на основе которой знание одной матрицы позволяет построить другую.
Пример 5.8. Проиллюстрируем выполнение соотношений 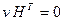 и
и 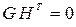 для кода (5, 3). Порождающая матрица и транспонированная матрица проверок имеют вид:
для кода (5, 3). Порождающая матрица и транспонированная матрица проверок имеют вид:
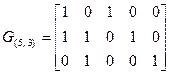
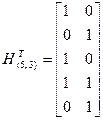
Вычисляем их произведение:

Здесь элементы матрицы Sij размерности (3х2) вычисляются следующим образом:
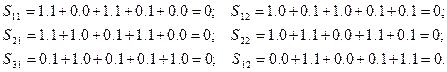
Таким образом:
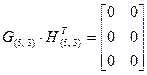
Пусть на приемную станцию системы передачи данных поступила комбинация (1 1 1 1 1). Каким образом можно установить факт наличия ошибок в комбинации?
Во-первых, проверить соответствие информационных и проверочных элементов в соответствии с правилом их формирования:
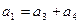 или
или 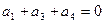 и
и 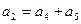 или
или 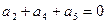 .
.
Для принятой комбинации получаем
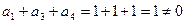
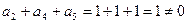 .
.
По результату этой проверки делаем вывод о том, что в принятой кодовой комбинации имеются ошибки.
Этот же самый процесс выявления соответствия принятой комбинации коду (5, 3) формализуется вычислением:

Проверочное соотношение дает ненулевой синдром, указывающий на наличие ошибок в принятой комбинации.
Для рассматриваемого кода (5, 3):
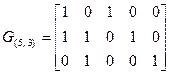 ,
, 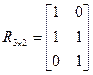 ,
, 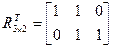 .
.
Используя свойство 5.4. получаем:


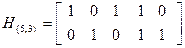 ,
,
| |||
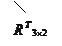 | |||
что полностью совпадает с матрицей, полученной в примере 5.7.
 2014-02-13
2014-02-13 3649
3649