Метод сопряженных направлений

Градиентный метод второго порядка.

Для квадратичных функций можно создать градиентный метод, при котором время сходимости будет конечным и равно числу переменных n.

Назовем некоторое направление 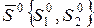и 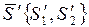сопряженными по отношению к некоторой положительно определенной матрице Гесса H, если выполняется:

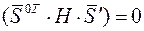Если ,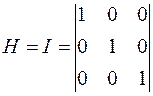

Тогда 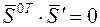т.е.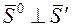

Значит при единичной H, сопряженное направление означает их перпендикуляр.

В общем же случае H неединичная. В общем случае сопряженность – это применение матрицы Гесса к вектору 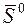- означает поворот этого вектора на некоторый угол и его растяжение или сжатие.

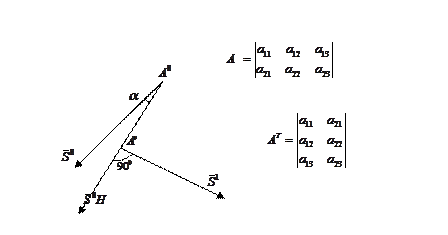
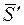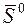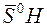а теперь вектору вектор ортогонален т.е. сопряженность это не ортогональность векторов и , а ортогональность повернутого вектора т.е. и .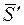

Пример.

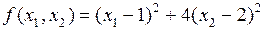
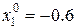
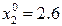
Зададим из точки 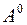любое направление 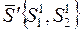. Пусть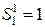

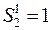
По верхнему extr рассекаем вертик. пл., 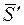-её след. Найдем min 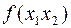на направлении . Это нам уже знакомо по методу МНС - метод наискорейшего спуска.

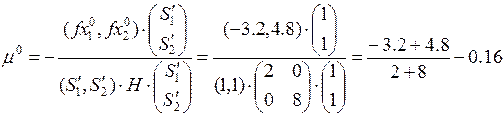
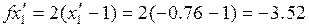
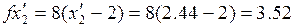
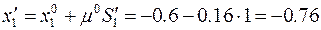
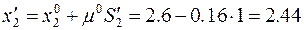
Т.е. шагнули от extr. Это неважно. Определим направление 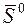, сопряженное к .

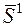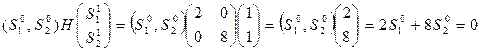
Зададимся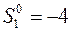

По направлению 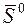ищем extr 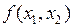, но так чтобы 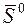проходило через точку 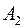(пунктир).

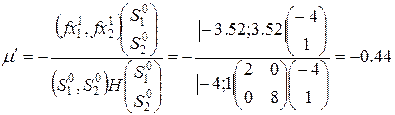
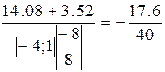, тогда

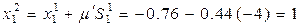
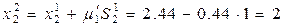
Т.е .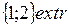

Таким образом, за 2 итерации для квадратичных функций мы попали в extr.