Шаг
Определяем в начальной точке проекции градиента
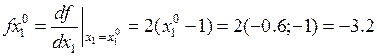
4) 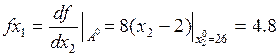
По направлению антигр. 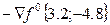 построим плоскость П2, перпендикулярную горизонтальной плоскости
построим плоскость П2, перпендикулярную горизонтальной плоскости 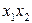 . Это плоскость пройдет через точку А0 и пересчет экстремальную поверхность
. Это плоскость пройдет через точку А0 и пересчет экстремальную поверхность 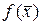 по экстремальной линии
по экстремальной линии 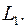
Уравнение этой линии с учетом выражения (2) (ибо вдоль неё мы и должны сделать 1-ую итерацию) имеет вид
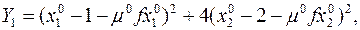 где
где
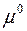 пока неизвестно. Понятно, что раз мы ищем минимум, то перед
пока неизвестно. Понятно, что раз мы ищем минимум, то перед 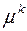 в (2) мы должны брать знак минус.
в (2) мы должны брать знак минус.
Выбираем 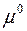 оптимальным т.е. таким, чтобы переместится из точки А0 в минимум экстремальной кривой т.е. в точку А1 за один шаг. Для этого найдем
оптимальным т.е. таким, чтобы переместится из точки А0 в минимум экстремальной кривой т.е. в точку А1 за один шаг. Для этого найдем 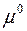 из выражения
из выражения
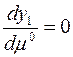
И так 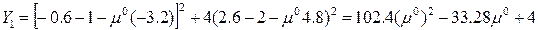
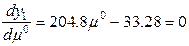
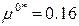
После этого найдем координаты экстремума рассматриваемой кривой т.е. координаты точки А1, по формуле (2)
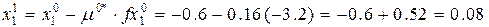
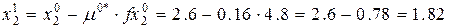
Это сделана одна итерация
2 шаг Принимаем точку А1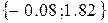 за начальную и все повторим
за начальную и все повторим
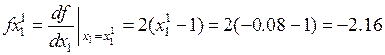
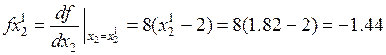
По направлению антиградиента 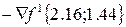 строим вертикальную площадь П2, которая пересечет горизонтальную площадь
строим вертикальную площадь П2, которая пересечет горизонтальную площадь 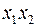 по линии L2, а экстремум поверхность
по линии L2, а экстремум поверхность 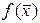 по экстремальной линии, уравнение которой запишем
по экстремальной линии, уравнение которой запишем 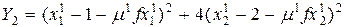 или
или
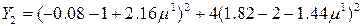 или
или
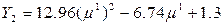
Найдем оптимальное значение 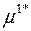
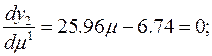
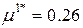
Тогда координаты экстремальной точки А2 в плоскости П2 по формуле (2) будут
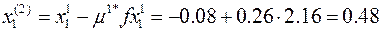

3 шаг Принимаем точку А2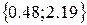 за начальную и проводимую 3-ую итерацию и т.д.
за начальную и проводимую 3-ую итерацию и т.д.
Этот алгоритм сходится за бесконечное число шагов. Однако, поскольку точность расчетов, т.е. точность поиска экстремума на практике известна в каждом конкретном случае, т.е. точность поиска экстремума на практике известна в каждом конкретном случае, то число шагов конечно.
Точность, как и в методе Гаусса Зейделя, можно задаваться по величине самой функции 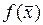 или по координатам.
или по координатам.
Нанесем на наш чертеж рис. 1
|

|
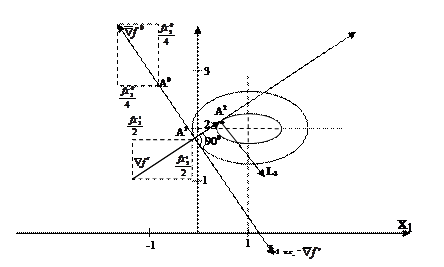
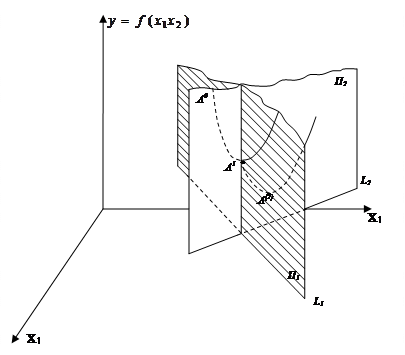 рис. 1
рис. 1
линии равного уровня. Поскольку в нашем случае 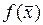 - квадратичная функция (сепарабельная), то оси фигур линии равного уровня (т.е. главные оси эллипсов) будут параллельны осям координат.
- квадратичная функция (сепарабельная), то оси фигур линии равного уровня (т.е. главные оси эллипсов) будут параллельны осям координат.
Мы уже знакомы с методом «Г-З», поэтому нас не должен удивлять тот факт, что частные экстремумы, т.е. точки А1, А2 и т.д. расположены в точках касания направлений градиентов L1, L2 с линией равного уравнения. Но что характерно для метода наискорейшего спуска, так тот факт, что если 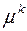 выбираются оптимальным образом, то углы между L1 и L2, L2 и L3 и т.д. получаются прямыми. Отметим, что это только в случае, когда
выбираются оптимальным образом, то углы между L1 и L2, L2 и L3 и т.д. получаются прямыми. Отметим, что это только в случае, когда 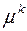 выбрано оптимальным. Возникает вопрос нельзя ли формализовать метод наискорейшего спуска, хотя бы для квадратичных функций? Оказывается можно.
выбрано оптимальным. Возникает вопрос нельзя ли формализовать метод наискорейшего спуска, хотя бы для квадратичных функций? Оказывается можно.
Пусть задано уравнение поверхности 220порядка в общем виде.
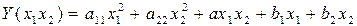
Проекции градиента на координате оси легко получить:
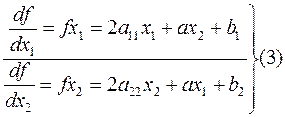
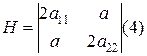
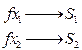
Возьмем произвольные направления 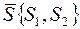 - не обязательно на градиенту и запишем уравнение параболы, получающейся в сечении поверхности
- не обязательно на градиенту и запишем уравнение параболы, получающейся в сечении поверхности 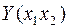 вертикальной плоскостью, проходящей по направлению
вертикальной плоскостью, проходящей по направлению 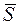 (как в разобранном примере, только там
(как в разобранном примере, только там 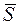 было направлением градиента).
было направлением градиента).
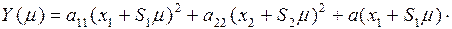
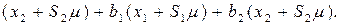
Раскроем скобки, сделаем приведение подобных и из уравнения 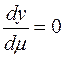 , найдем оптимальное значение
, найдем оптимальное значение 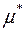 .
.
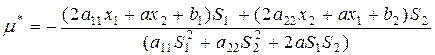
или, с учетом (3) и (4) перепишем это выражение в матричной форме.
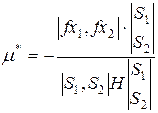

Получим выражение для оптимальности 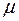 по произвольному направлению
по произвольному направлению 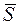 . Если же за направление
. Если же за направление 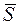 взять напрвлеие градиента (антиградиента), то получится:
взять напрвлеие градиента (антиградиента), то получится:
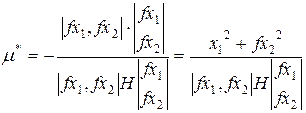
Это для n=2.
Для многомерного случая:
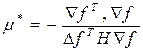
Метод наискорейшего спуска имеет ряд модификаций, например 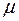 задается в виде некоторого ряда и его не надо.
задается в виде некоторого ряда и его не надо.
Для квадратичных функций сепарабельной и несепарабельной можно записать формулу
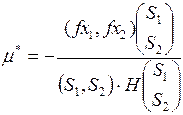
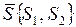
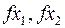 - проекции градиента;
- проекции градиента;
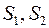 - направления.
- направления.
Н – матрица Гесса.
Для поиска маке /При поиске min знак –заменяем на +/
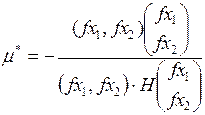 для n =2
для n =2
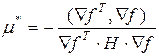 для любых n
для любых n
Пример.
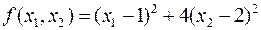
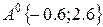
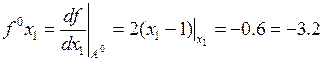
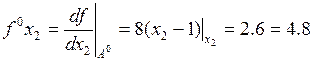

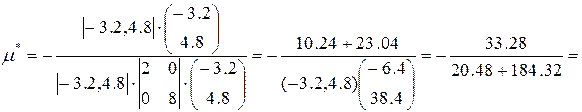
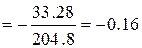
 2014-02-13
2014-02-13 665
665